UIT2201: Tutorial Set 1 (Spring 2013)
(Solution Sketch to Selected Problems)
** NOT TO BE GIVEN TO FUTURE UIT2201 STUDENTS **

Solution sketches are provided as guidelines only. Do not think of them as *model answers*. As you have noticed from our tutorial discussions, there can be many answers and approaches. So keep an open mind. (More importantly, DO NOT CIRCULATE these solution sketches.)
T1-D3: (Tourist Problem, Special Case -- one place only) --- SOLUTION SKETCH
Only 1 day is needed for this special case. The graph is an empty graph, namely, has vertices, but no edges. So, all vertices can be coloured the same colour!

T1-D4: (Tourist Problem) -- conflict generation --- SOLUTION SKETCH
(a) 6 tourists will introduce 15 edges. Why? Many different explanations:

  1. Number of edges = 0 + 1 + 2 + 3 + 4 + 5 = 15
  2. Number of edges = (Sum the degree of vertices) / 2 = (6 * 5) / 2 = 15.
  3. Number of different ways to choose two vertices (out of 6) to connect: 6C2 = (6*5) / (2*1) = 15
(b) For n places, the number of edges introduced is n(n-1)/2

T1-D5: [Tourist Problem] -- Algorithm (Discussion)
Actually, we did not get to discuss this in class.

Later in the course, we will discover that, as of today, all scientists (CS, Math, Physicists, Engineering, etc) in the world still do not have a good algorithmic solution to this problem. At least, nothing that is substantially better than the try all possible solutions, and choose a best one type algorithm. But these algorithm take forever to run (reference: T5-Q5).

T1-Q1: (10 points) [Origami and Computing] -- (Outcome!)
View the photos of your Origami on UIT2201 Facebook page at here.

T1-Q3: (10 points) [Job Scheduling Problem] -- SOLUTION SKETCH

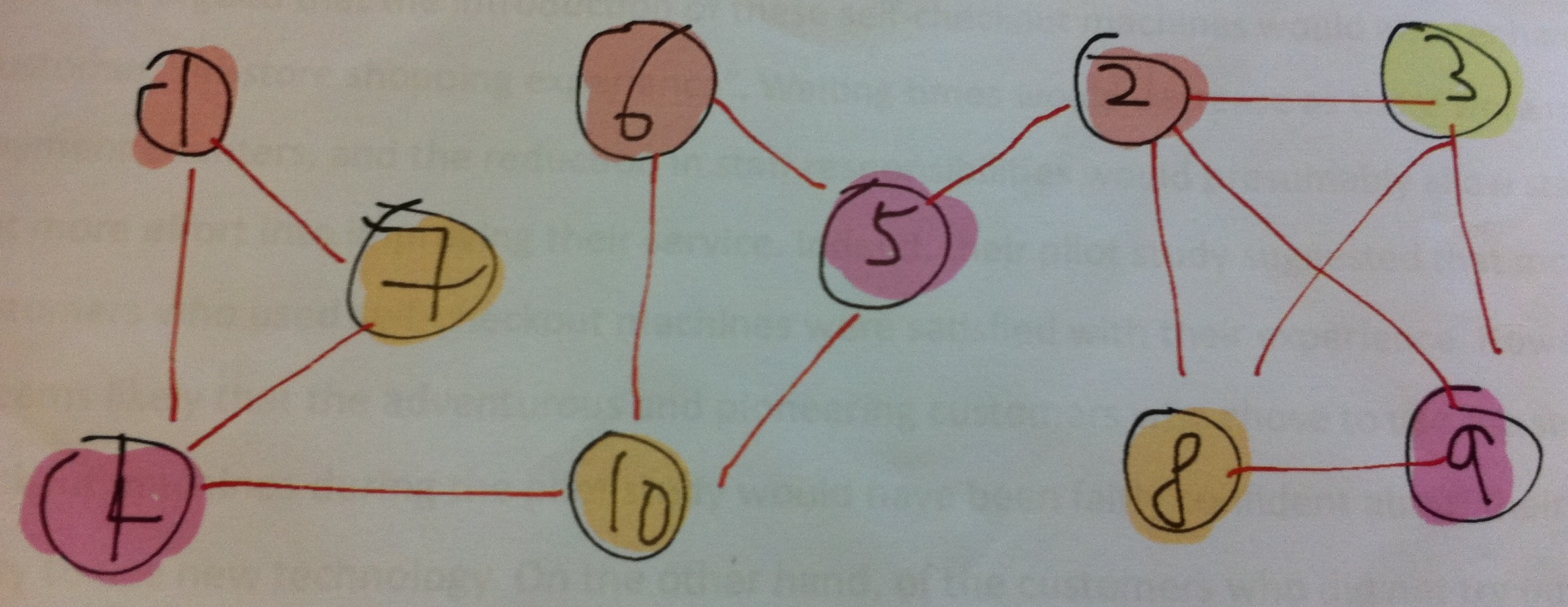
(a) Model with an undirected graph (with vertices and edges). The vertices represent (model) the jobs The edges represent (model) the time conflicts -- connect two vertices x and y if the corresponding jobs Jx and Jy overlaps in time, namely, share a common time duration. Then, we get the graph shown below (courtesy of Kristen):


Note: If you graph is "messy", you can "move" your vertices around so that you can "see" a less cluttered graph.

(b) Graph can be coloured using 4 colours. So, the jobs can be assigned to 4 workers.
(Note: There are many ways to colour the graph, so if you used 5 colours, try other ways to colour so you need only 4!)

T1-Q4: (10 points) [Tourist Problem. The Good and the Bad] -- SOLUTION SKETCH
(a) 2. How? Many ways actually. One simple way is to have everyone visit the same two places. Then it is trivially done in 2 days. But people can visit different places and still complete in 2 days. However, the general condition is more complicated.

I generally do NOT put up discussion of A-problems in these pages -- in order not to alarm some students.
However, since A1 is not my typical A-problems, I will make an exception. Please do not be too worried if you do not fully understand the solution sketch for this A-problem.

A1: Actually, this should really be T1-Q4 (b).
6.
Here, we try to make as large a clique as we can with each tourist creating a different edge. With 20 students, we can make 20 edges. We can get cliques of size 6 (15 edges), but not of size 7 (21 edges).

UIT2201: CS & IT Revolution; (Spring 2013); A/P Leong HW
[Prints well with A4-page-offsets l=r=b=t=0.5"=12.7mm]