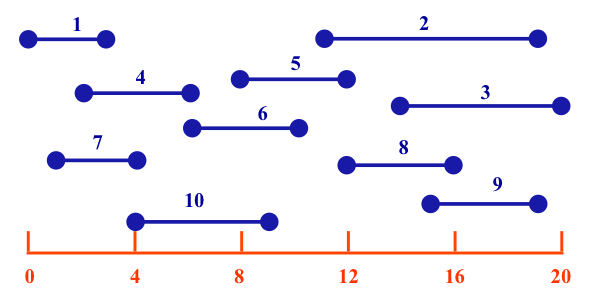
J3 = [14,20], J4 = [02,06],
J5 = [08,12], J6 = [06,10],
J7 = [01,04], J8 = [12,16],
J9 = [15,19], J10 = [04,09],
(D-Problems discussed on Wednesday, 16-Jan-2013)
(Q-Problems due on Friday, 18-Jan-2013, 5:00pm)
T1-D1: [e-Greeting Cards] (Do this before the tutorial on Wednesday!)
(a) Search for an e-greeting card web-site
and send a greeting card to yourself and to me.
Also browse around a few of these web-sites to learn about the
other services that are provided by these web-sites.
(Note: The NUS e-card site is at
http://www.nus.edu.sg/ecards/.
Use online search for others.)
(b) Compare a few different e-greeting card web-sites.
List out some attributes that you may want to compare them with.
How does the different sites fare with respect to your
comparison attributes?
T1-D2: (Getting the Scratch Software Framework)
This year, in UIT2201, we (students and instructor) embark
on an interesting and fun journey -- using the Scratch
(http://scratch.mit.edu)
software framework to learn about algorithms and
for project.
(a) Your first task is to download the scratch software
and install it on your laptop/desktop.
(b) Read the simple free how-to guide and download
some of the (numerous) free Scratch programs and test them out.
T1-D3: [Tourist Problem -- one place only]
Consider the special case of the Tourist Problem v1.0
in which each tourist only want to visit one place
(of course, different tourists may want to visit different places).
Give a very simple (no brainer)
method to schedule the buses for this special case.
How many days does it take to complete the schedule?
Does it matter how many tourist there are?
T1-D4: [Tourist Problem -- conflict generation]
In the Tourist Problem example, Aaron wants to visit three places
SZG, BG, JB.
In the graph model, the three places are modeled as three vertices.
In addition, three edges are introduced into the graph to
represent the conflicts among these vertices.
(a) If a tourist (call him X) wants to visit 6 different places,
how many edges will be introduced into the graph to represent
the conflicts?
(b) What if X wants to visit m places (where m is some integer)?
T1-D5: [Tourist Problem]
In class, we showed several colourings of the graph, but we
did not explain how the colouring step was done.
In the language of CS, what is the algorithm that was
used to do the colouring step.
Based your own intuition,
give a few possible algorithms for colouring a graph.
Note: Give step-by-step instructions in English,
that can be precisely and uniquely executed
by yourself (and your classmates).
T1-Q1: (10 points) [Origami and Computing]
Algorithms have often been compared with Origami
-- the art of paper folding.
(a) For this problem, you should do a paper folding of an object
of your choice --- but it should involve more than
15 basic folding steps.
You are to submit the finished product (the folded origami piece).
(b) Along with the finished product, please also submit the instructions
for folding it onto IVLE folder called "T1-Q1-Origami".
(If the instructions are from a book, snap a picture and save as file,
if it is web-page, save it as a document (pdf or ps file).
If you do not know how to save as pdf or ps file, then snap a picture
and save as file.) If it is youtube video, just list the url.
(Hint: If you are not an origami person,
go online to search for origami instructions or
find an origami book in the library.
There are plenty available.)
T1-Q2: (10 points) [CS/IT Enabled Solution to World Problems]
In the past decade, there has been many efforts
to leverage CS/IT to help solve global/world problems (big or small),
whether by companies, NGOs, individuals, or citizen groups.
Do a search for a specific example of this and write a short report
on this. Be specific about what the problem is, how CS/IT has help
to solve this problem, and how it might be further improved, where
appropriate. Limit your report to at most to at most 1.5 pages,
font size 12, 1.5 line spacing. Give the source(s) of your information.
T1-Q3: (10 points) [Job Scheduling Problem]
In this problem, you are given a list of 10 jobs --
J1, J2,.., J10.
The kth job
Jk = [s, e]
has a start time s
and an end time e (for k=1,2,..,10).
See an example in the diagram below.
|
J1 = [00,03],
J2 = [11,19],
J3 = [14,20], J4 = [02,06], J5 = [08,12], J6 = [06,10], J7 = [01,04], J8 = [12,16], J9 = [15,19], J10 = [04,09], |

|
You have a list of workers, and
you want to assign these jobs to a minimum number of workers.
Each worker can do any number of jobs as long as the jobs do not overlap in time. (For this problem, you can assume that a worker can start on
a new job immediately after finishing a previous job.
So, jobs J7 and J10 can be assigned to the same worker, if necessary.)
We shall solve this job scheduling problem using graph coloring.
We first model this problem with a graph.
In the graph model, each job is modeled as a node in the graph.
(a) Explain carefully how the edges in the graph are defined and
show the graph model you get for this job scheduling instance.
(b) What is the minimum number of workers needed to complete all
the jobs?
T1-Q4: (10 points) [Tourist Problem. The Good and the Bad]
Suppose that the entire UIT2201 class are the tourists
in the Tourist Problem v1.0 (assume there are 20 students in the class).
Suppose that each of you must visit exactly two places,
but you are free to choose whichever two places you like.
(a) (The Good) You want to help the tour company finish scheduling all
the trips as soon as possible (ASAP).
And so all 20 of you conspire together and
work out a strategy to choose the places
in such a way that it will take
the minimum number of days to schedule all the trips.
What is the minimum number of days needed to complete all the trips?
And how should the students choose the places?
A1: [Continued from Problem T1-Q4]
(b) (The Bad) Now, suppose that you want to force the tour company
finish scheduling all the trips as late as possible (ALAP).
So, all 20 of you conspire together and
work out a strategy to choose the places
in such a way that it will take
the maximum number of days to schedule all the trips.
What is the maximum number of days that you can "impose"
on the tour company?
And how should the students choose the places?