Memory Model

Learning Objectives

At the end of this sub-unit, students should

• understand the memory model of assignment.
• know how to reason about assignment.

Mental Model

Some of the behavior of assignments can be quite difficult from looking only at the code. This is especially true if this is your first programming experience. A mental model will help you significantly. We will show two mental models.

1. Visual: Box and arrow diagram.
2. Textual: Memory model.

These are intended to illustrate the behavior step by step. Eventually, the hope is for you to be able to reason about any code without the explicit use of these mental model. In the case of box and arrow diagram, we will show how arrow comes into play when we touch on the more general compound data type.

All of these mental model are still simplifications in a way, but they allow for a more explicit explanation. So they are still useful, which is why we introduce them here. Unfortunately, since there is a "time" component that is difficult to show except by using animation, we will approximate them using tabs instead. You should click on the tabs to show the state after each assignment.

The explanation of these mental model will be done using examples as opposed to give a clear instruction on how to evaluate them. This approach is preferrable as we have already given a step by step procedure to perform assignment. So what is needed is really an illustration of what happened behind scene.

Box and Arrow Diagram

The first mental model we will explain is the box and arrow diagram which we have used before to show a variable.

Re-Assignment

We will start with a simple example of re-assignment.

x = 0
print(x)   # 0 is printed
x = x + 1
print(x)   # 1 is printed

0
1

How do we reason this more precisely with box and arrow diagram? The tabs below shows the state of the program as box and arrow diagram after each assignment. We also added note to show what is happening in more details. The behavior we are showing is the more complete behavior. Simplifications are often done and we encourage you to do simplify them once you have enough experience.

Note that we start with no box and no arrow. This represents the initial state of Python program¹.

After Line 1After Line 3

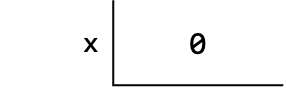
Since there is no variable named x yet, we will create one and store the value 0. Now, print(x) will be evaluated to print(0).

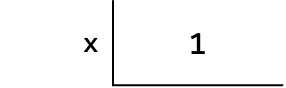
As the intermediate step, we will need to evaluate x + 1 first. This is done using the previous state where x = 0. Then we create a new box containing 1 and redirect the arrow to this new box.

Swap

The second illustration is the case of swapping.

x, y, z = 0, 1, 2
print(x, y, z)   # 0 1 2 is printed
x, y = y, x
print(x, y, z)   # 1 0 2 is printed

0 1 2
1 0 2

After Line 1After Line 3

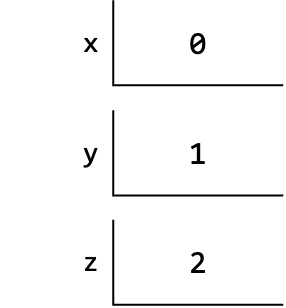
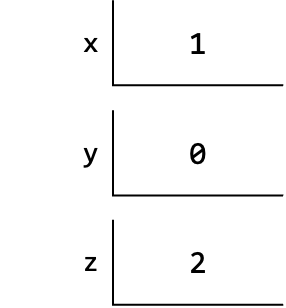
Incorrect Swap

This is an incorrect swap with extra variable.

x, y = 0, 1
print(x, y)   # 0 1 is printed
x = y
y = x
print(x, y)   # 1 1 is printed

0 1
1 1

We will cross the old value to show that there are changes even if the change is to the same value.

After Line 1After Line 3After Line 4

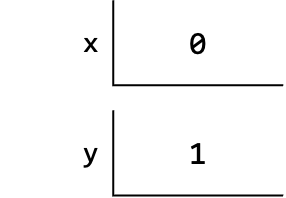
Memory Model Diagram

If you feel that drawing box and arrow diagram is complicated because you may not always have access to a blank paper, we will introduce the textual approach below. A state of a program is captured by the mapping from a name to a value.

{ name1 ↦ value1 , name2 ↦ value2 , ... }

This way, we can actually show the state as a comment on the code. We will insert the state in before and after every line of code to show the changes. Let us see this in action. Hopefully, it is clear from the comments and the state what the expected behavior is.

Re-AssignmentSwapIncorrect Swap

# { }
x = 0
# { x ↦ 0 }

# { x ↦ 0 }
print(x)   # 0 is printed
# { x ↦ 0 }

# { x ↦ 0 }
x = x + 1  # rhs is x + 1 and evaluated with x ↦ 0 to be 0 + 1
# { x ↦ 1 }

# { x ↦ 1 }
print(x)   # 1 is printed
# { x ↦ 1 }

0
1

# { }
x, y, z = 0, 1, 2
# { x ↦ 0 , y ↦ 1 , z ↦ 2 }

# { x ↦ 0 , y ↦ 1 , z ↦ 2 }
print(x, y, z)   # 0 1 2 is printed
# { x ↦ 1 , y ↦ 0 , z ↦ 2 }

# { x ↦ 0 , y ↦ 1 , z ↦ 2 }
x, y = y, x
# { x ↦ 1 , y ↦ 0 , z ↦ 2 }

# { x ↦ 1 , y ↦ 0 , z ↦ 2 }
print(x, y, z)   # 1 0 2 is printed
# { x ↦ 1 , y ↦ 0 , z ↦ 2 }

0 1 2
1 0 2

# { }
x, y = 0, 1
# { x ↦ 0 , y ↦ 1 }

# { x ↦ 0 , y ↦ 1 }
print(x, y)   # 0 1 is printed
# { x ↦ 0 , y ↦ 1 }

# { x ↦ 0 , y ↦ 1 }
x = y
# { x ↦ 1 , y ↦ 1 }

# { x ↦ 1 , y ↦ 1 }
y = x
# { x ↦ 1 , y ↦ 1 }

# { x ↦ 1 , y ↦ 1 }
print(x, y)   # 1 1 is printed
# { x ↦ 1 , y ↦ 1 }

0 1
1 1

---

1. To be more precise, it is not exactly blank because there are built-in functions. However, we will often omit those. ↩