List and Function

Learning Objectives

At the end of this sub-unit, students should

• understand that mutability persists across function call.
• understand the behavior of list methods.
• know how to use list for a more efficient computation.

Aliasing Across Function

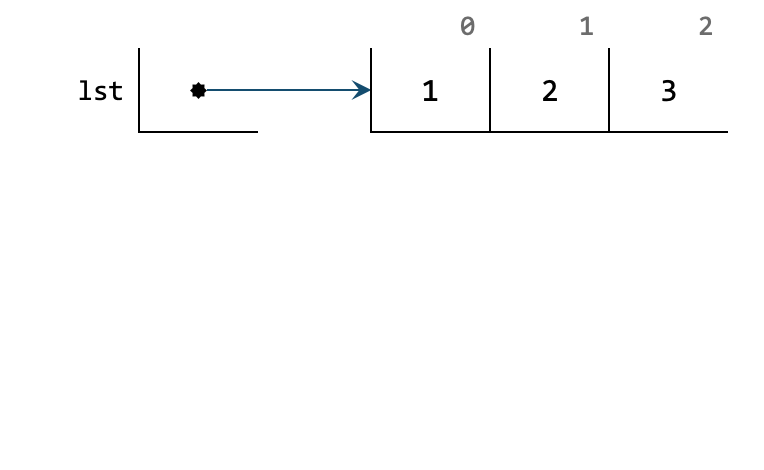
Because aliasing is a somewhat pervasive problem, we should embrace it. One of the advantage of a mutable list is that a function need not need additional memory. This also shows that aliasing persists across function calls. As an example, we will use a very simple function to update a list at a particular index with a value.

def update(lst, idx, val):
  lst[idx] = val

>>> lst = [1, 2, 3]
>>> lst
[1, 2, 3]
>>> update(lst, 0, 9)
>>> lst
[9, 2, 3]

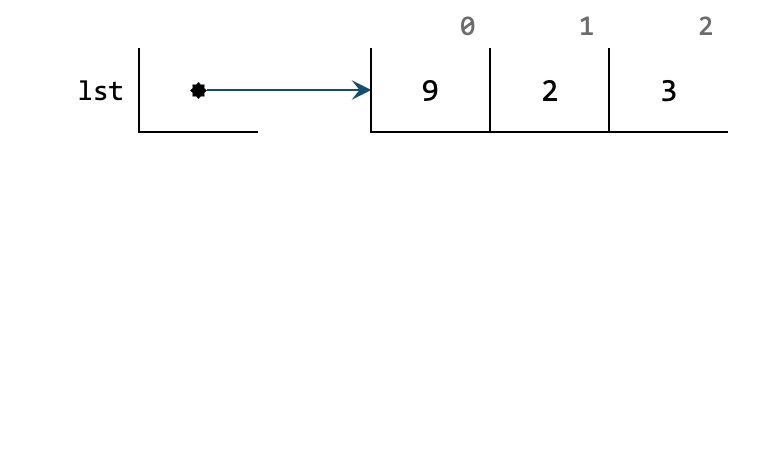
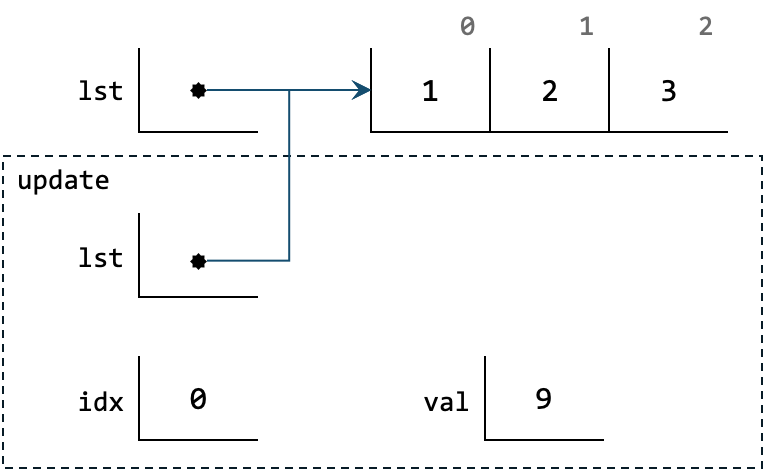
The function has no return value. So it will return None. However, it will update the input list lst as seen above. How can we reason about this? The answer is --as usual-- box-and-arrow diagram. We put the scope of the function update within a dashed box. This means that the variable lst inside update is different from the variable lst outside. Since the lst outside is not inside any dashed box, it is a global variable. 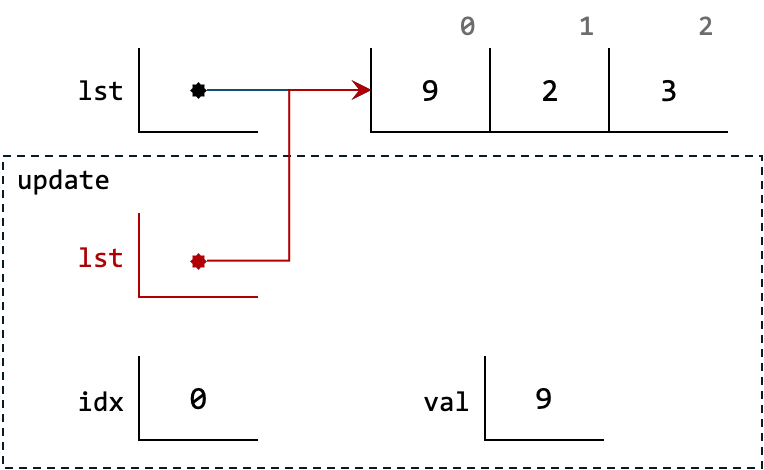At the end of the function call, the dashed box is removed as the function has finished.

After Line 1 (IDLE)After Line 1 (update)After Line 2 (update)After Line 4 (IDLE)

Benefit of Aliasing

We can benefit from this aliasing. Consider a function which is commonly called map. However, our map is different from the built-in map because the built-in version requires us to accept a function as parameter and we have not explain about higher-order function. We further simplify our map to simply multiply all the elements in the list by n.

Multiply by n

Problem Description

Given a list lst, we want to multiply all the element in the list by n. The function should not return anything and it should simply update the list lst without creating any new list.

Task

Write the function map_n(lst, n) to multiply all the element in the list lst of integer by n.

Assumptions

• lst is a list of integer, potentially empty (i.e., len(lst) >= 0).
• n is an integer.

Restrictions

• You are NOT allowed to convert to other data types.
• You are NOT allowed to create other sequence.

First, we decompose the problem as follows.

• Enumerate all the valid positive index of lst.
  • For each index idx, we update lst[idx] by multiplying it with n.

Multiply by n

def map_n(lst, n):
  for idx in range(len(lst)):
    lst[idx] = lst[idx] * n

That is the solution, it is short and it works simply because any update to lst inside the function map_n can be seen by the caller. This is the advantage of aliasing. But why not just use tuple and return a new tuple? Let us compare this solution with a solution for tuple.

Multiply by n (Tuple)

def map_n_tuple(tpl, n):
  res = ()
  for elem in tpl:
    res = res + (elem * n,)
  return res

The way we are going to compare it is to find out the time it takes to compute both. Luckily, there is a Python module called timeit that we can use. You do not have to understand how to use it, we will show the two codes below and post the timing on our machine. You may get a different timing on your computer.

Timing for List

# map function for list
def map_n(lst, n):
    for idx in range(len(lst)):
    lst[idx] = lst[idx] * n



# initialize a list of 100,000 elements
lst = list(range(100_000))

# run with timing
print(timeit.timeit('map_n(lst, 2)',
                    globals=globals(),
                    number=10))

0.03335060004610568

Timing for Tuple

# map function for tuple
def map_n_tuple(tpl, n):
    res = ()
    for elem in tpl:
    res = res + (elem * n,)
    return res

# initialize a tuple of 100,000 elements
tuple = tuple(range(100_000))

# run with timing
print(timeit.timeit('map_n_tuple(tpl, 2)', 
                    globals=globals(),
                    number=10))

131.50360940000974

That is a major improvement! Using list, our runtime is almost 4000x faster than using tuple. For now, we cannot do a proper analysis of the timing. Instead, we will show the graph of the two run with different number of elements.

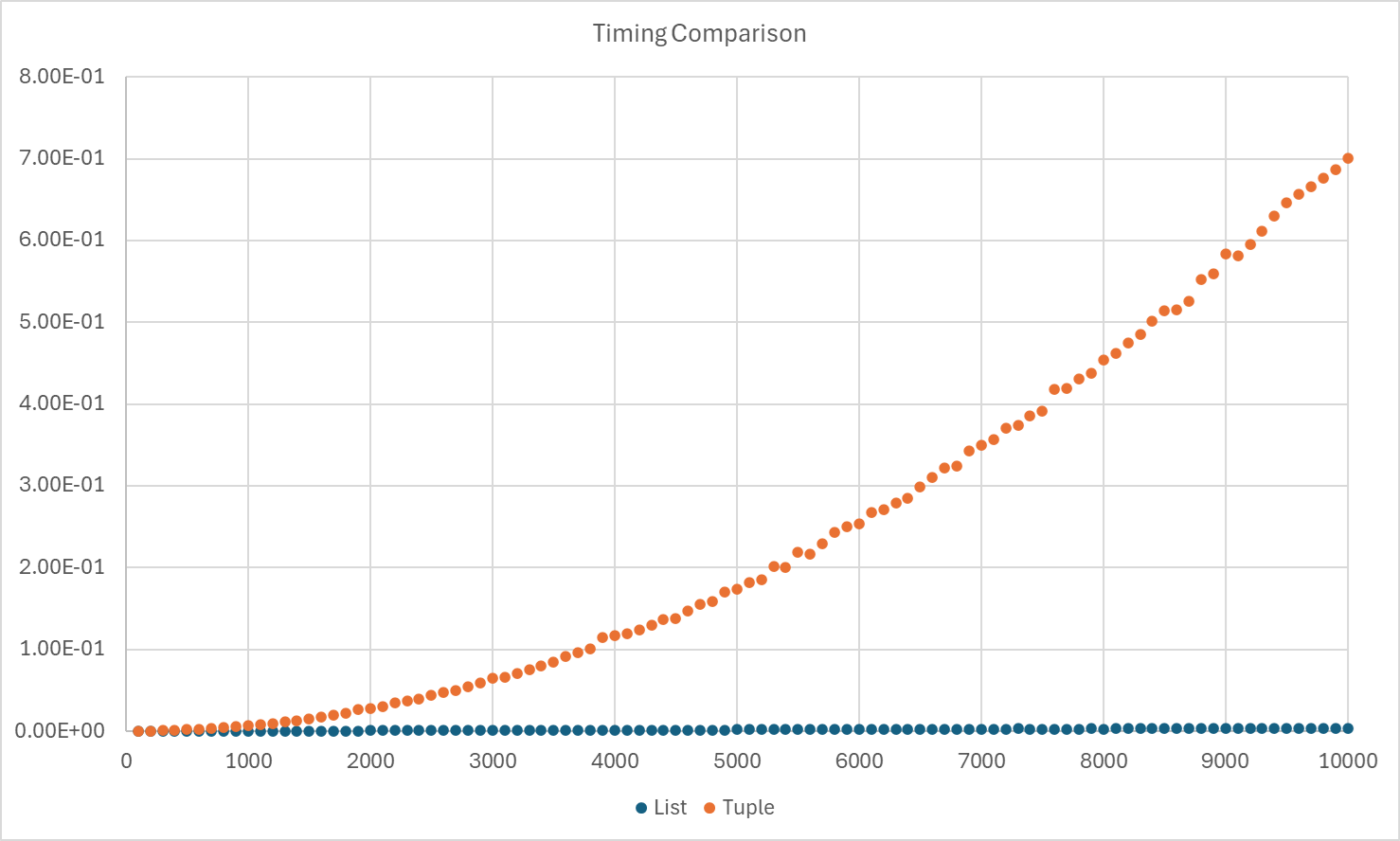
The timing for tuple is shown in orange while the timing for list is shown in blue. Hopefully that convinces you of the benefit of using list and why it is worth it to understand aliasing and all its pitfalls.

To see why using tuple is very inefficient, we can see that we are actually constructing a new tuple in each iteration. The assignment res = res + (elem * n,) takes the old tuple res and copy before adding a new element elem * n. This copying takes a lot of time when the tuple gets larger. On the other hand, lst[idx] = lst[idx] * n in the case of the list does not require copying.

List Methods

We may argue that this is cheating because the number of element in the resulting sequence is the same as the original sequence. In general, that is not always the case. So tuple is still much more useful in general. Luckily, the inventor of Python has thought of this too and provided useful methods to update a list without creating a new list.

We call this methods instead of function because of a crucial difference: the way it is invoked. Given a function fn, we invoked it by fn(arg). On the other hand, a method mth written for a particular data type T can be invoked using an object of that data type obj by obj.mth(arg). The difference is subtle, it is called the dot notation.

Consider a tuple tpl. We know that a tuple is immutable. So if we invoked fn(tpl, arg), we know that tpl will never be updated. The only way we can update tpl is via assignment in the caller tpl = fn(tpl, arg). For instance, the map_n_tuple above.

>>> tpl = (1, 2, 3)
>>> map_n_tuple(tpl, 2)
(2, 4, 6)
>>> tpl # unchanged
(1, 2, 3)
>>> tpl = map_n_tuple(tpl, 2)
>>> tpl
(2, 4, 6)

On the other hand, we know that map_n can modify lst even without assignment.

>>> lst = [1, 2, 3]
>>> lst
[1, 2, 3]
>>> map_n(lst, 2)
>>> lst # changed
[2, 4, 6]

We will take this idea further. We want to remove some elements that does not satisfy a certain property. This is commonly known as filter and again, there is a higher-order built-in function called filter.

Keep Multiple of n

Problem Description

Given a list lst, we want to keep only elements that are multiple of n.

Task

Write the function filter_n(lst, n) to create a new list that consists only of elements in lst that are multiple of n.

Assumptions

• lst is a list of integer, potentially empty (i.e., len(lst) >= 0).
• n is an integer.

Restrictions

• You are NOT allowed to convert to other data types.

First Attempt

As our first attempt, we will show a very simple way to solve this by accumulation.

Keep Multiple of n

def filter_n(lst, n):
  res = []
  for elem in lst:
    if elem % n == 0:
      res = res + [elem]
  return res

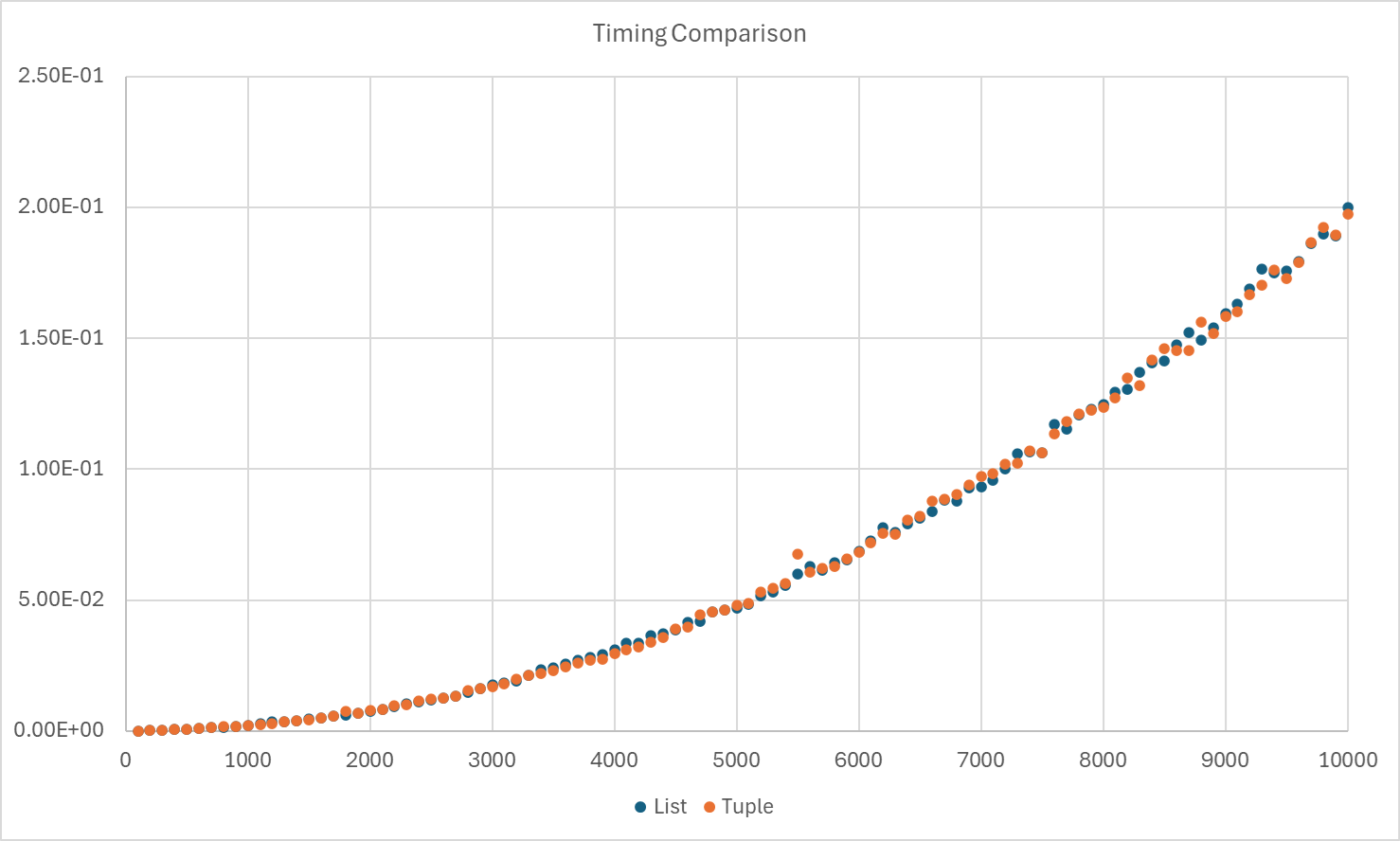
This is no different from the tuple version. Even the timing comparison is similar. How can we improve?

Second Attempt

To improve the timing, we need to introduce our first list method. This is called append. This method has the following property when we invoke it with lst.append(obj).

• It accepts an object obj.
• It does not return anything.
• It updates the list lst by adding a new box at the end of the list containing obj.

Let us look at how we can use this. Note that the argument obj is taken as it is and appended to the very end of the list. This obj can even be another list. But instead of concatenating, we simply put the entire list argument as the last element. This is shown in Line 7 to Line 9.

List Append

>>> lst = [1, 2, 3]
>>> lst
[1, 2, 3]
>>> lst.append(4)
>>> lst
[1, 2, 3, 4]
>>> lst.append([5, 6, 7])
>>> lst
[1, 2, 3, 4, [5, 6, 7]]

Common Mistake

The second property above is critical. This function does not return anything but only updates the list that appears before the dot (i.e., the lst in lst.append(obj)). So if we accidentally assigning the result back to lst, we will get None because as we learnt quite a while ago that a function that does not return anything returns None.

>>> lst = [1, 2, 3]
>>> lst = lst.append(4)
>>> lst # nothing is printed for None
>>> print(lst)
None

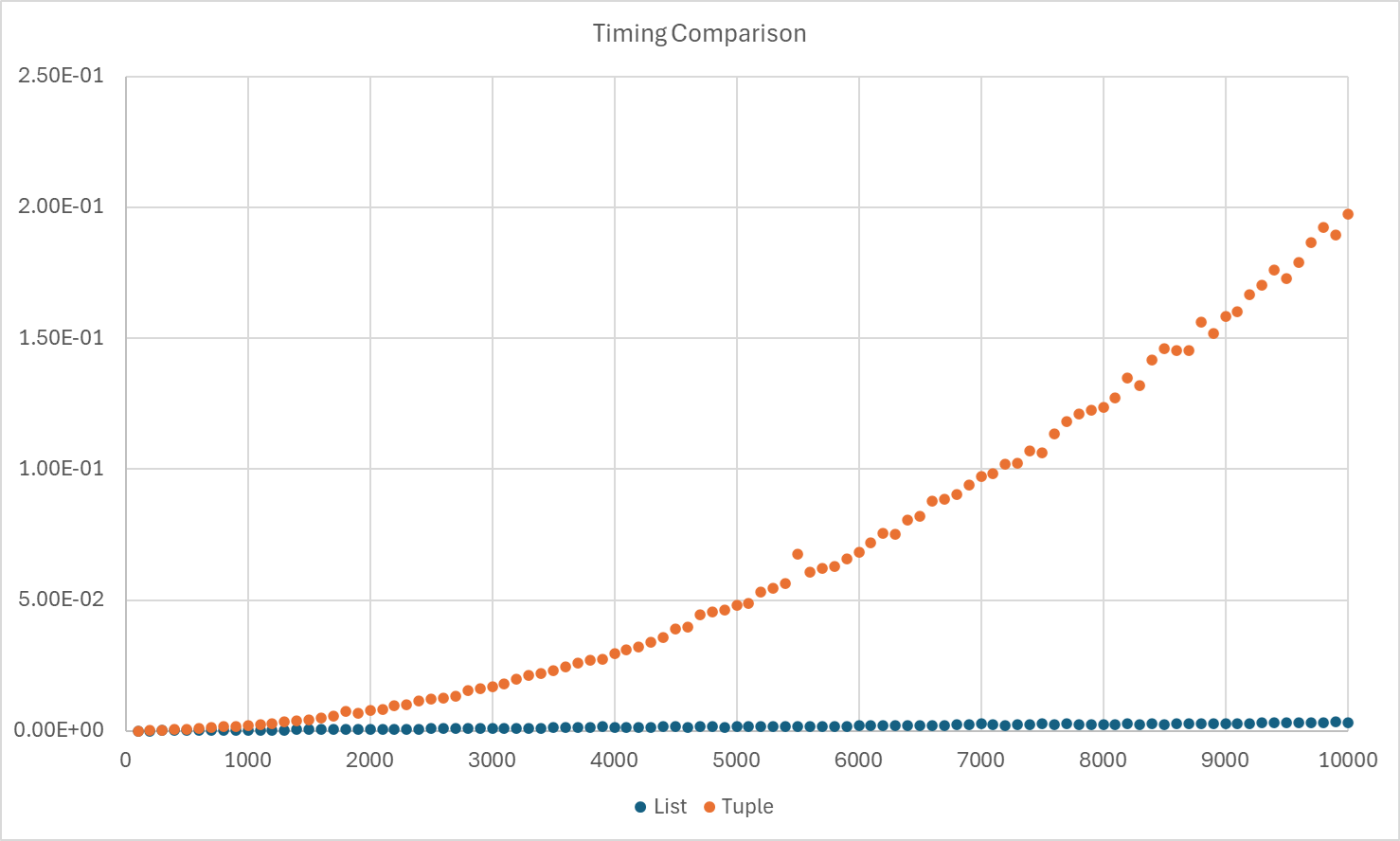
Now that we know this append method, we can improve our solution by using res.append(elem) instead of res = res + [elem]. This is a simple update with major implication to the speed.

Keep Multiple of n

def filter_n(lst, n):
  res = []
  for elem in lst:
    if elem % n == 0:
      res.append(elem)
  return res

Other List Methods

append is not the only list method. We introduced first as it was beneficial. We will now introduce other useful list methods and show the example usage with a list lst.

Method	Description
lst.append(obj)	Updates the list lst by adding the element obj to the end of the list. The function does not return anything.
lst.extend(seq)	Updates the list lst by adding all the elements from the sequence seq to the end of the list one by one. The function does not return anything.
lst.remove(obj)	Updates the list lst by removing the first occurrence of obj from lst. The function does not return anything. The function produces an error if obj is not in the list lst.
lst.insert(idx, obj)	Inserts obj into the list lst, shifting all elements from index idx and above to the right by one index. The function does not return anything.
lst.pop()	Removes and returns the last element of lst.
lst.pop(idx)	Removes and returns the element of lst at index idx.
lst.copy()	Returns a shallow copy of lst. This is similar to our copy function.
lst.clear()	Clears the list lst. The function does not return anything.

Note that unless we specify that the method returns something, the method returns None. To make the example short, we will use three columns for our example. The left column will be the code, the middle column will show the value of s, and the right column will show the value of t after each line is executed.

Code

s = [1, 2, 3, 4]
t = s.copy()
s.reverse()
s.insert(0, 1)
s.pop()  # returns 1
s.pop(1) # returns 4
s.insert(1, 2)
s.remove(2)
s.clear()

Value of s

[1, 2, 3, 4]
[1, 2, 3, 4]
[4, 3, 2, 1]
[1, 4, 3, 2, 1]
[1, 4, 3, 2]
[1, 3, 2]
[1, 2, 3, 2]
[1, 3, 2]
[]

Value of t

​
[1, 2, 3, 4]
[1, 2, 3, 4]
[1, 2, 3, 4]
[1, 2, 3, 4]
[1, 2, 3, 4]
[1, 2, 3, 4]
[1, 2, 3, 4]
[1, 2, 3, 4]

Notice how t does not change because we keep on updating s. Since t is a shallow copy, it is no longer aliased with s.

Augmentation

There is an optional knowledge on other kinds of assignments about augmented assignment. One of the augmented assignment we have is the += operator. We mentioned that the semantic of var += expr is the same as var = var + (expr). Unfortunately, this is not exactly correct in the case of list.

To illustrate, we can try running the following two codes and compare the runtime. Try with a large number to see a significant difference in the runtime.

• Augmented

  ---

  lst = []
  for i in range(100_000):
    lst += [i]
  print(len(lst))
  

  100000
  

• Rewritten

  ---

  lst = []
  for i in range(100_000):
    lst = lst + [i]
  print(len(lst))
  

  100000
  

Why is there a big difference in the runtime? Using +=, we get an almost instant result. On the other hand, using the supposedly equivalent rewritten code we get a significantly slower code. The reason is because lst += [item] is translated into lst.append(item) for list.

How does Python know it is working with a list? It does not really have to. Behind the scene, all var += expr is actually translated to var.__iadd__(expr). Then, in the implementation, __iadd__ for list will simply call append. __iadd__ is called a magic/special/dunder method¹.

Loop Catastrophe

Another problem with mutability is the interaction with loop, especially for loop. We will discuss two common problems involving list and loop. Some of the behavior may cause infinite loop. In such cases, we recommend pressing Ctrl+C to stop the execution of your Python code in IDLE.

Remove

The first common problem is caused by removal of elements from a list without properly updating the index during iteration. Consider the following problem of removing all elements greater than n from a list. One way to do this is to loop through the index of the list and invoke the lst.pop(idx) method if the element at index idx is greater than n. Study the following code.

Incorrect Solution #1

def remove_greater(lst, n):
  for idx in range(len(lst)):
    if lst[idx] > n:
      lst.pop(idx)

At a glance, the code looks correct. But a quick test run will show that it produces an error as long as there is at least one element removed.

>>> lst = [5, 1, 2, 3]
>>> remove_greater(lst, 4)
IndexError

What is happening? We can try to trace the execution with the trace table and see the behavior. As this is the first time we will be tracing for-loop with range(...), we will remind you that the range(...) is only evaluated once. So we will first evaluate this and we get a sequence of [0, 1, 2, 3]. Given the sequence produced, we know that there must be 4 iterations and we will construct the trace table appropriately.

Iteration	lst2	idx2	lst[idx]	lst[idx] > n	lst4
1	[5, 1, 2, 3]	0	5	True	[1, 2, 3]
2	[1, 2, 3]	1	2	False
3	[1, 2, 3]	2	3	False
4	[1, 2, 3]	3	IndexError

In this case, we cannot use for-loop and we need to actually use while-loop. The reason for using while-loop is that we need to keep on updating the number of elements in the list at the beginning of the loop. If we use for-loop, the expression range(len(lst)) is computed once. And because the number of element in lst is updated during the iteration, the value we used at the beginning is incorrect. This leads to the error we see. So let us update this to while-loop and see the effect.

Incorrect Solution #2

def remove_greater(lst, n):
  idx = 0
  while idx < len(lst):
    if lst[idx] > n:
      lst.pop(idx)
    idx = idx + 1

>>> lst = [5, 1, 2, 3]
>>> remove_greater(lst, 4)
>>> lst
[1, 2, 3]
>>> lst = [5, 1, 5, 2, 5, 3]
>>> remove_greater(lst, 4)
>>> lst
[1, 2, 3]

This looks correct, why is it marked as wrong? Here, the problem is more subtle. Although we will not get an error, there is a case where the code will not correctly remove elements. We will illustrate with the worst-case example, try to find a more specific example.

>>> lst = [5, 5, 5]
>>> remove_greater(lst, 4)
>>> lst
[5]

There is a value that we did not managed to remove. Construct the trace table and figure out the problem.

The solution is that we need to selectively increment the index only if there is no removal of element from the list. We do this selective increment by actually decrementing the index when we perform removal. That way, we can always have an increment as the last statement in the loop. Since the increment and the decrement cancels out, the net effect is no increment.

Correct Solution

def remove_greater(lst, n):
  idx = 0
  while idx < len(lst):
    if lst[idx] > n:
      lst.pop(idx)
      idx = idx - 1
    idx = idx + 1

>>> lst = [5, 1, 2, 3]
>>> remove_greater(lst, 4)
>>> lst
[1, 2, 3]
>>> lst = [5, 1, 5, 2, 5, 3]
>>> remove_greater(lst, 4)
>>> lst
[1, 2, 3]
>>> lst = [5, 5, 5, 5, 5, 5, 5]
>>> remove_greater(lst, 4)
>>> lst
[]

Append

The second common problem is caused by trying to add more elements into the list. This is typically done by append but may also be done with extend. Weirdly, this problem is caused by the fact that although the expression expr is evaluated only once in for var in expr, the iterable collection used still share the same underlying list. So if we add more element to the end of the underlying list, the iterable collection will also have more element. This may cause the iteration to play catch-up with the append.

We should warn that the following code does not terminate. In short, be careful with this behavior and avoid updating the list within a loop. It is harder to make mistakes if we create new list to store the result.

Append Inside For-Loop

lst = [1, 2, 3]
for elem in lst:
  lst.append(elem)

Press Ctrl+C to terminate the execution of your code on IDLE.

---

1. Dunder is a shorthand for double-under which indicates that the method starts with double-underscore. ↩