This project was inspired by the Mario AI that went viral recently. The AI was designed to learn how to play Super Mario Bros game using a genetic algorithm, popularly known as Neural Evolution through Augmenting Topologies(NEAT). The logic behind NEAT is that by using a method to carefully selectively breed good performing Neural nets, and by mutating them slightly, the model can learn to optimize any black-box function effectively.

A NEAT model playing Super Mario Bros.

This inspired me to try out some basic reinforcement learning models on my own. I read about Markovian Decision Process based RL models from a really good book, “Reinforcement Learning: An Introduction” by Richard S. Sutton and Andrew G. Barto. Among the models presented in the book, I used a model based on Monte Carlo, which utilizes the positive properties of Dynamic Programming and Monte-Carlo models(also MDP based).

For the purpose of creating an environment for the RL model, I used an open-sourced Nintendo Entertainment System(NES) simulator FCEUX v2.2.2, that supports Lua scripting to read/write RAM map and automate joy-pad inputs. A famous Lua library named Torch was used for some mathematical computations. I reused some code of the MarI/O NEAT implementation by Seth Bling to read RAM map and setup the environment for my RL model. In this blog, I have tried to explain the concept of Monte Carlo learning model and my implementation of a modification to this model that learns to play Mario.

Markov Decision process is a discrete time stochastic control process, that satisfies the condition that the state the system moves to, when the agent takes an action, depends only on the current state and not on the entire path of states it took to reach the current state. If the dynamics of the system, i.e. the transition probabilities p(s’|s,a) of reaching some state s’ when an action a was taken at some state s, is completely know, we can find the probability of the system being in a state using the theory for Markov Decision Processes. If for each s to s’ state transition, the agent is given a reward r(s,s’), and the agent wants to select actions for each state so that the net long-term λ-discounted rewards is maximized, then our problem reduces to finding an optimal Policy (mapping of states to actions) that gives the best long-term rewards. An iterative method of finding the optimal Policy for such an MDP is called Dynamic Programing, and is explained in Chapter 4 of this book. In Dynamic Programing, we iteratively calculate the optimal Value function, i.e. the function giving net expected returns for the optimal Policy starting from the input state, and using this optimal value function, the optimal policy is calculated.

blog-image

An example MDP with three states corresponding actions with transition probabilities.

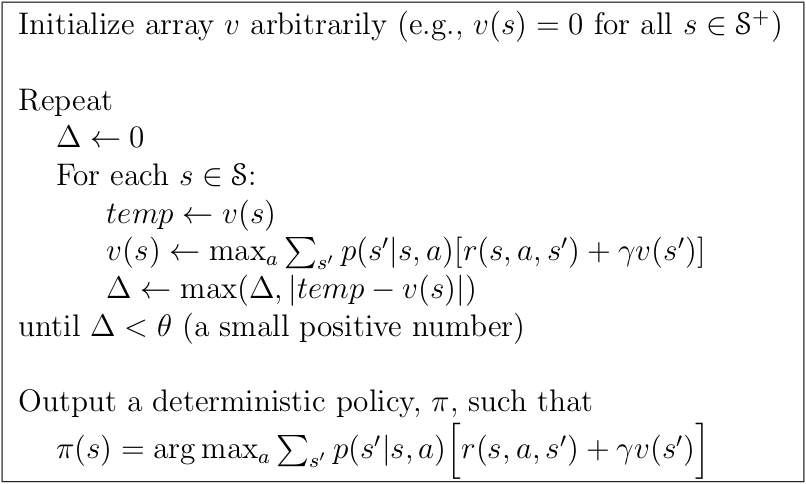
blog-image

Psuedocode of Dynamic Programming model for finding optimal Policy.

The environment of Mario is a bit tricky. We don’t completely know the transition probabilities of any action(Buttons to press on joy-pad) taken for any state(the grid of block world surrounding Mario). In other words, we don’t know beforehand what next screen input would we see (and with what probability) if we decide to make Mario jump on the current screen input. To tackle this problem, we will use another RL method that works on similar grounds as Dynamic Programming, called Monte-Carlo method. The difference in this method is that instead of having using the transition probabilities(which is unavailable in our case) to find the Value function, it runs episodes of environment simulations to approximate the optimal Quality function (similar to Value function), using which, it computes the optimal Policy. The benefit of this method is that we don’t have to know the dynamics of the environment beforehand, just a way to extract data from this dynamic environment by running episodic simulations (which can be done in our case). A shortcoming of this method however is that it requires “Exploring Start”, i.e. the freedom to start randomly from different states for different episodes, which is tough to implement(randomly initialize Mario from any place in the game) in our case.

blog-image

Psuedocode of Monte Carlo model with exploring starts for finding optimal Policy.

We can do away with the requirement of having exploring start by using an ϵ-soft policy, i.e. regardless of whatever optimal policy we know of yet, their is always a small probability ϵ that a non-optimal random action is taken at each state, which helps the algorithm to keep on exploring new optimal policies. The psuedocode of this algorithm is given below.

blog-image

Psuedocode of ϵ-soft policy Monte Carlo algorithm.

The above model can be used for training our Mario AI. Let’s first create an environment for the model, and then we will proceed on to the implementation of the model.



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115



player1 = 1
BoxRadius=6
InputSize = (BoxRadius*2+1)*(BoxRadius*2+1)
TIMEOUT=50

-- Import the requires libraries.
function set_imports()
  require("torch")
end

-- Function to set a particular level and world.
function set_level(world,level)
  memory.writebyte(0x75F,world)
  memory.writebyte(0x75C,level)
  memory.writebyte(0x760,level)
end

-- Function to set the global Mario location.
function getPositions()
  marioX = memory.readbyte(0x6D) * 0x100 + memory.readbyte( 0x86 )
  marioY = memory.readbyte(0x03B8)+16
  screenX = memory.readbyte(0x03AD)
  screenY = memory.readbyte(0x03B8)
end

-- Function to get a particular tile with respect to Mario.
function getTile(dx, dy)
  local x = marioX + dx + 8
  local y = marioY + dy - 16

  local page = math.floor(x/256)%2
  local subx = math.floor((x%256)/16)
  local suby = math.floor((y - 32)/16)
  local addr = 0x500 + page*13*16+suby*16+subx

  if suby >= 13 or suby < 0 then
          return 0
  end

  if memory.readbyte(addr) ~= 0 then
          return 1
  else
          return 0
  end
end

-- Function to get the enemy tile locations.
function getSprites()
  local sprites = {}
  for slot = 0,4 do
    local enemy = memory.readbyte( 0xF+slot)
    if enemy ~= 0 then
      local ex = memory.readbyte( 0x6E + tonumber(slot))* 0x100 + memory.readbyte( 0x87 + tonumber(slot))
      local ey = memory.readbyte( 0xCF + slot) + 24
      sprites[#sprites+1] = {["x"]=ex,["y"]=ey}
    end
  end
  return sprites
end

-- Function to create a Box around Mario and return an input vector of the same. Free Free tile is 0, enemy tile is -1 and block tile is 1.
function getInputs()
  getPositions()
  sprites = getSprites()
  local inputs = {}

  for dy=-BoxRadius*16,BoxRadius*16,16 do
    for dx=-BoxRadius*16,BoxRadius*16,16 do
      inputs[#inputs+1] = 0

      tile = getTile(dx, dy)
      if tile == 1 and marioY+dy < 0x1B0 then
        inputs[#inputs] = 1
      end

      for i = 1,#sprites do
        distx = math.abs(sprites[i]["x"] - (marioX+dx))
        disty = math.abs(sprites[i]["y"] - (marioY+dy))
        if distx <= 8 and disty <= 8 then
          inputs[#inputs] = -1
        end
      end
    end
  end
  return inputs
end

-- Function returns true if Mario is in air.
function isInAir()
  if memory.readbyte(0x001D) ~= 0x00 then
    return true
  else 
    return false 
  end
end

-- Function returns true of Mario dies.
function isDead ()
  if memory.readbyte(0x000E) == 0x0B or memory.readbyte(0x000E) == 0x06 then
    return true;
  else
    return false;
  end
end


-- Function to create a save state at the start of a selected world and level.
function set_state ()
  while(memory.readbyte(0x0772)~=0x03 or memory.readbyte(0x0770)~=0x01) do
    set_level(01,01)
    emu.frameadvance()
  end
  level_start = savestate.object(1)
  savestate.save(level_start)
end

We need to call set_state() before the start of the execution of the model, to create a loadable save point at the beginning of the game level. The function getInputs() is used to get an input vector of size InputSize that describes the state of the process. Each state of the MDP process is determined using the tiles surrounding Mario. The function cuts a box of edge size 2*BoxRadius around Mario and returns it in a vectored form. A tile in the box is represented by 0 if it is an empty space, 1 if it is a block space(like ground or brick-tiles) and -1 if their is an enemy on the tile. Now lets look at the Monte Carlo implementation.



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27



function set_values()
  Returns={}
  Policy={}
  TIMEOUT=50
  TIMEOUT_AIR=10
  EPSILON=0.05
end

function getHashReturns(Inputs, Action)
  return getHashPolicy(Inputs).."->"..Action
end

function getHashPolicy(Inputs)
  local I_value=""
  for i=1,#Inputs do
    I_value=Inputs[i]..I_value
  end
  return I_value
end

function getReturnsForPair(Inputs,Action)
  if Returns[getHashReturns(Inputs,Action)]==nil then
    return 0
  else
    return Returns[getHashReturns(Inputs,Action)][1]
  end
end

I created a hash function that converts the Input into a string and then hashes it. This is for quick retrial of policies based on the hashing string. The getHashReturns(Inputs, Action) concatenates the Action as a string to the Input hash. The function getReturnsForPair(Inputs,Action) returns the Returns of the Input, Action pair.



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41



function getButtonsForAction(Action)
  local action_hash=Action
  b_str=""
  local buttons = {["A"]=false,["B"]=false,["up"]=false,["down"]=false,["left"]=false,["right"]=false}
  if action_hash%2==1 then
    buttons["right"]=true
    buttons["left"]=false
    b_str=b_str.."right, "
  else
    buttons["right"]=false
    buttons["left"]=true
    b_str=b_str.."left, "
  end
  action_hash=math.floor(action_hash/2)
  if action_hash%2==1 then
    buttons["up"]=false
  else
    buttons["up"]=true
    b_str=b_str.."up, "
  end
  action_hash=math.floor(action_hash/2)
  if action_hash%2==1 then
    buttons["B"]=true
    b_str=b_str.."B, "
  else
    buttons["B"]=false
  end
  action_hash=math.floor(action_hash/2)
  if action_hash%2==1 then
    buttons["A"]=true
    b_str=b_str.."A, "
  else
    buttons["A"]=false
  end
  action_hash=math.floor(action_hash/2)
  if not action_hash==0 then
    eum.message("error, set button for hash didn't receive correct value\n")
  end
  emu.message(b_str)
  return buttons
end

The Action parameter is an integer value, whose binary representation gives the combination of buttons to press. For simplicity and ease of training, I have added some constraints that at any time either Left or Right button must be pressed and Down button is never pressed. The function returns a dictionary of Buttons with their corresponding boolean values indicating if the button is pressed.



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21



function generateAction(Inputs)
  local action_taken
  g_str=""
  if Policy[getHashPolicy(Inputs)]==nil then
    action_taken=torch.multinomial(torch.ones(1,16),1)
    action_taken=action_taken[1][1]
    g_str=g_str..",new "
  else
    g_str=g_str..",found "
    local x,y=torch.max(torch.Tensor(Policy[getHashPolicy(Inputs)]),1)
    action_taken=torch.multinomial(torch.Tensor(Policy[getHashPolicy(Inputs)]),1)
    action_taken=action_taken[1]
    if action_taken==y[1] then
      g_str=g_str..",taken "
    else
      g_str=g_str..",not taken "
    end
  end
  action_taken= action_taken-1
  return action_taken
end

The above function generates an action based on the Input state and the current Policy. If the state is being seen for the first time, a random action is taken. If the state is not new, an action is chosen based on the Policy. Since the Policy is an ϵ-soft Monte Carlo, their is always a non-zero probability of choosing a non optimal action for any Input state.



1
2
3
4
5
6



-- The reward function.
function getReward()
  local time_left=memory.readbyte(0x07F8)*100 + memory.readbyte(0x07F9)*10 + memory.readbyte(0x07FA)
  local dist = marioX
  return time_left*dist
end

The above function is the reward function being called at the end of each episode to get the reward. The reward is the product of distance traveled and the time remaining. We want the AI to reach the end of the level as quick as possible.



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50



function run_episode()
  savestate.load(level_start)
  maxMario=nil
  local memory={}
  local state = {}
  local action_for_state=nil
  
  while true do
    state=getInputs()
    action_for_state=generateAction(state)
    joypad.set(player1,getButtonsForAction(action_for_state))
    emu.frameadvance()
    memory[#memory+1]={state,action_for_state}
    
    if isDead() then
      emu.message("Dead")
      break
    end

    local timeout=TIMEOUT
    local timeout_air=TIMEOUT_AIR
    local long_idle=false

    while(getHashPolicy(getInputs())==getHashPolicy(state)) do
      joypad.set(player1,getButtonsForAction(action_for_state))
      emu.frameadvance()
      if timeout==0 then
        long_idle=true
        break
      end
      timeout = timeout-1
    end

    while(isInAir()) do
      joypad.set(player1,getButtonsForAction(action_for_state))
      emu.frameadvance()
      if timeout_air==0 then
        break
      end
      timeout_air = timeout_air-1
    end

    if long_idle then
      emu.message("Killed Due to timeout")
      break
    end

  end
  return memory
end

The above function runs an episode of the game. It reloads to the start point (which is saved while initializing the environment). The function repetitively takes the input state of the environment and takes an action based on Policy. I added a timeout to end episode if it stays idle for too long. Also I disabled taking an action while in air to reduce the size of the memory list. The function keeps track of all the Input, Action pairs seen in the form of a memory list, and returns this list at the end of the episode.



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50



function start_training()
  local Policy_number=1
  while true do
  
    run_memory=run_episode()
    run_reward=getReward()
    print("Policy is "..Policy_number)
    print("Run is "..i)
    print("Reward->"..run_reward)
    print("memory size->"..#run_memory)
    local new_states=0
    for i=1,#run_memory do
      local hashed_pair=getHashReturns(run_memory[i][1],run_memory[i][2])
      if Returns[hashed_pair]==nil then
        new_states = new_states + 1
        Returns[hashed_pair]={run_reward,1}
      else
        Returns[hashed_pair][1]=(Returns[hashed_pair][1]+run_reward)/(Returns[hashed_pair][2] + 1)
        Returns[hashed_pair][2]=Returns[hashed_pair][2] + 1
      end
    end
    print("Number of New States is "..new_states)
  

    for i=1,#run_memory do
      
      local max=-1
      local optimal_action=-1
      if Policy[getHashPolicy(run_memory[i][1])]==nil then
        Policy[getHashPolicy(run_memory[i][1])]={}
      end
      
      for j=0,15 do 
        if getReturnsForPair(run_memory[i][1],j) > max then
          max=getReturnsForPair(run_memory[i][1],j)
          optimal_action=j
        end
      end
            
      for j=0,11 do
        if j==optimal_action then
          Policy[getHashPolicy(run_memory[i][1])][j+1]= 1 - EPSILON +EPSILON/11
        else
          Policy[getHashPolicy(run_memory[i][1])][j+1]= EPSILON/11
        end
      end
    end
    Policy_number=Policy_number+1
  end
end

The above function trains the AI by running episodes and updating the Policy. It gets the memory of the episode and then iterates through all the state-action pairs, updating the Returns dictionary. Then it iterates through the memory again to update the Policy for the states seen in the last episode. Since the policy is an Epsilon soft policy, we have to keep a minimum non-zero probability for all actions.



1
2
3
4
5
6



function init ()
  set_imports()
  set_state()
  set_values()
  emu.speedmode("maximum")
end

The init() function is called before start_training() function to set the imports, the environment, to initialize the dictionary and global values, and to set the emulator speed. Now all that is left is to call the functions and observe the training of AI.



1
2



init()
start_training()

Here’s the first 1.5 minutes of the training of the model. We can clearly see how the AI improves as it discovers better paths.

First 1.5 minutes of ϵ-soft Monte Carlo training run.

The model was able to complete Level 1 of World 1 after around 3 hours of training. Though this model is not as strong as NEAT model, which trains the AI to be able to play any level once trained, this model is simple enough for beginners to try and get impressive results.

The code for this project is open sourced, and can be found here.