Particle Swarm Optimization balancing Cart-Pole
CartPole balancing problem is considered one of the benchmark problems in reinforcement learning. The problem requires to design a model that learns how to balance a pole vertically on a cartwheel. For simplicity, the system is considered to be two dimensional and the cartwheel is allowed to move only in one dimension. OpenAI gym provides simple, easy to use, environments for many such benchmark problems. The CartPole environment allows two actions, +1 and -1, to be taken at any instant. This action corresponds to the direction of application of force on the cart. The observation taken at any instant of the environment is a tuple consisting of horizontal position, horizontal velocity of the cart, angle of inclination of the pole and velocity of the tip of the pole.
Swarm Intelligence Optimization is a very simple and extensively parallelize-able method for optimizing parameters of a model. This technique tries to mimic swarm behavior(like the behavior of a flock of birds) to reach the global optimal solution of an optimization problem. The benefit of this method over other optimization techniques however is that instead of trying to tune a single parameter (using gradient decent or back propagation for a neural network), it tunes a batch of parameters (each parameter can be imagined as a bird lying in a multidimensional coordinate) all at once, which converges to the global optimal solution(like a flock of birds gathering on a food source). Each parameter of the batch is updated, in an epoch, to move a small random distance towards either the best value coordinate of objective function it saw on it’s path(the best food source the bird knows about) or the best value coordinate that the batch observed on it’s path(the best food source the flock knows about).
Simple Particle Swarm(PSO) Implementation
Let’s start with a basic implementation of a single threaded implementation of swarm particle optimization. We will need the following imports.
1
2
3
4
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import copy
The following is a particle class, having three attributes namely position velocity and best position with corresponding getter and update functions, is used to create individual particles of the swarm. Each instance of this class has current position attribute which is updated, based on the velocity and time unit, on every call of update_velocity class function.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Particle(object):
def __init__(self, position,velocity):
self.position=copy.copy(position)
self.velocity=copy.copy(velocity)
self.best_pos=copy.copy(position)
def update_time_step(self,time_unit):
self.position+=copy.copy(self.velocity)*time_unit
def update_velocity(self,velocity):
self.velocity=copy.copy(velocity)
def update_best_position(self,position):
self.best_pos=copy.copy(position)
def get_position(self):
return copy.copy(self.position)
def get_best_position(self):
return copy.copy(self.best_pos)
def get_velocity(self):
return copy.copy(self.velocity)
Next we create a Swarm class that contains a set of instances of Particle class. An object of Swarm class will have attributes defining the properties of the swarm as a whole. The parameters of the init function is explained as follows:
- particle_count -> The number of particles in the swarm.
- inertia -> The inertia of each particle in the swarm. The greater the value of this parameter, the more each particle resists change in velocity.
- cognitive -> The cognitive weight of each particle. This parameter dictates the intent of a particle to go towards the best coordinate that it has seen in it’s path.
- social -> The social weight of each particle. This parameter dictates the intent of a particle to go towards the best coordinate that the entire swarm has seen as a group.
- random_position_generator -> The pointer to a function that gives a random position(N dimensional Numpy array) in the domain of interest. This function is used to initialize the position of the particles randomly on the domain.
- random_velocity_generator -> The pointer to a function that gives a random velocity vector(same dimension as the position). This function is used to initialize the velocity of the particles randomly.
- objective_function -> The pointer to the objective function that takes as input a position vector and gives the value at that point. The objective function is the function whose parameter is being optimized.
- alpha -> This parameter is used to tune the velocity sensitivity of the particles.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Swarm(object):
def __init__(self, particle_count,inertia,cognitive,social,random_position_generator,random_velocity_generator,objective_function,alpha):
self.swarm_best_pos=None
self.swarm_best_value=None
self.particles=[]
self.animation_position=[] #used for visualization purpose
self.particle_count=particle_count
self.alpha=alpha
self.inertia=inertia
self.cognitive=cognitive
self.social=social
self.objective_function=objective_function
for i in range(particle_count):
particle=Particle(random_position_generator(),random_velocity_generator())
self.particles.append(particle)
particle.best_value=self.objective_function(particle.get_position())
if ((self.swarm_best_value != None) or (self.swarm_best_value<self.objective_function(particle.get_position()))):
self.swarm_best_pos=particle.get_position()
The attributes of the Swarm class are initialized as shown above. Now we need a function to update these attributes at each unit time step. The following function of the Swarm class does this.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def epoch(self,time_unit):
swarm_position=np.zeros(shape=(0,2)) #used for visualization purpose
for particle in self.particles:
particle.update_time_step(time_unit)
particle.update_velocity((self.inertia*particle.get_velocity())
+(self.cognitive*np.random.uniform(0,self.alpha)*(self.swarm_best_pos-particle.get_position()))
+(self.social*np.random.uniform(0,self.alpha)*(particle.get_best_position()-particle.get_position())))
if(self.objective_function(particle.get_position())>self.objective_function(particle.get_best_position())):
particle.update_best_position(particle.get_position())
if(self.objective_function(particle.get_best_position())>self.swarm_best_value):
self.swarm_best_pos=particle.get_best_position()
self.swarm_best_value=self.objective_function(particle.get_best_position())
swarm_position=np.vstack([swarm_position, np.array(particle.get_position())]) #used for visualization purpose
self.animation_position.append(swarm_position) #used for visualization purpose
The function takes a parameter time_unit and allows the particles of the swarm to move freely, based on their velocities, for time_unit units of time. Then the function updates the velocities of the particles as shown. The best coordinates of the particles are changed if the new position gives a higher value of the objective function, and the group best coordinate and objective function value is also updated.
We define another class function of Swarm class which is called to plot the animation of the swarm converging in 2-D. This function is not at all necessary for implementation, and is only used to visualize the convergence.
1
2
3
4
5
6
7
8
9
10
def update_plot(self,i):
self.scat.set_offsets([np.array(self.animation_position[i])[:,0],np.array(self.animation_position[i])[:,1]])
return
def finish(self):
self.fig=plt.figure()
plt.axis([-2, 2, -2, 2])
self.scat=plt.scatter(np.array(self.animation_position[0])[:,0],np.array(self.animation_position[0])[:,1])
ani=animation.FuncAnimation(self.fig,self.update_plot,frames=xrange(len(self.animation_position)),interval=100)
plt.show()
Now all that is left is to create an object of swarm class and execute it for a fixed number of epochs. The following example shows how an object MySwarm of class Swarm is created and ran for 100 time units. Our objective function is negative of the euclidean distance from the origin.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
particle_count=5
inertia=0.79
cognitive=1.49445
social=1.49445
time_unit=1
alpha=0.2
def random_position_generator():
return np.random.uniform(-2,2,2)
def random_velocity_generator():
return np.random.uniform(-0.02,0.02,2)
def objective_function(position):
return -np.sqrt(np.mean(position**2))
MySwarm = Swarm(particle_count,inertia,cognitive,social,random_position_generator,random_velocity_generator,objective_function,alpha)
for i in range(100):
MySwarm.epoch(time_unit)
MySwarm.finish()
The following gif shows the output animation of the particles converging.
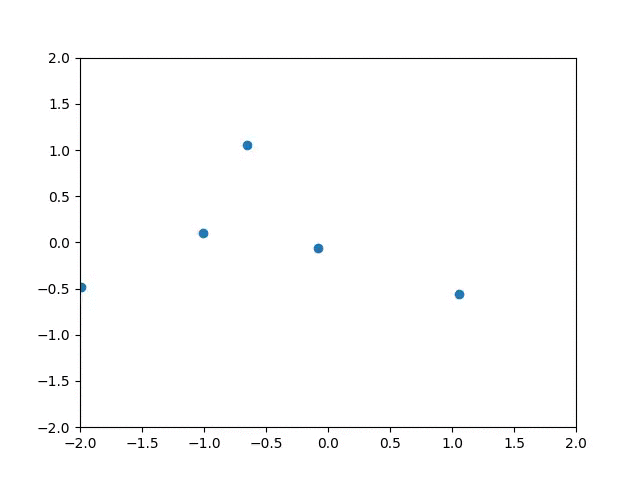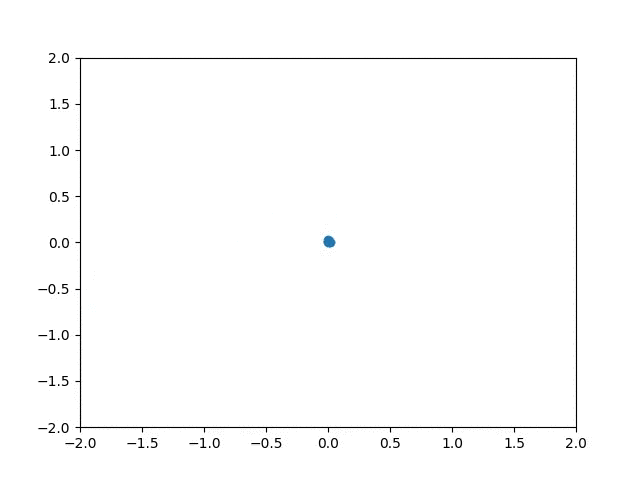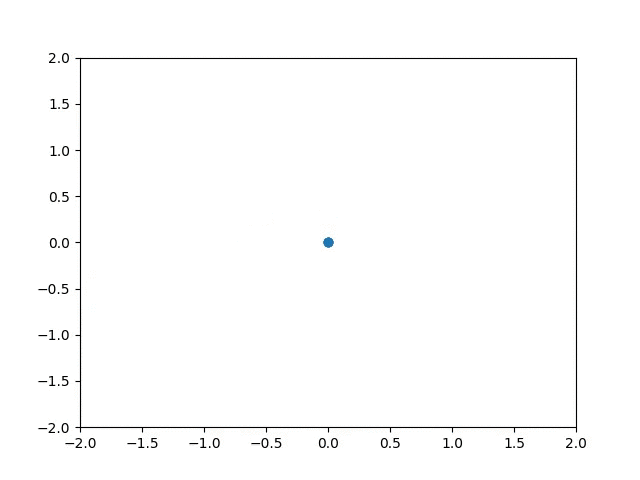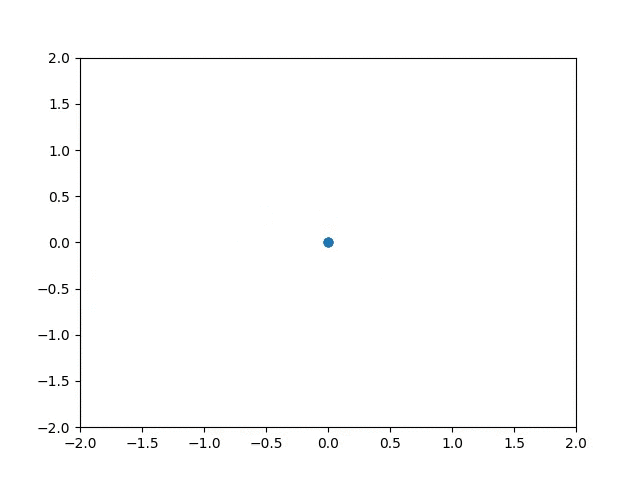
Swarm Optimization converging on (0,0)
A Parallel Processing implementation of Cart-Pole problem using PSO
Now that we know of a simple implementation and logic behind PSO, lets create a parallelized implementation of the same to solve the cart pole balancing problem. As mentioned above, we are going to use an openAI gym environment. Let’s first start with a single instance of a linear model optimizer for the problem. Since we ultimately want a parallel implementation, it would be better if we create a derived Process class to represent our EnvWorker class. We would need the following exports.
1
2
3
4
import gym
import time
from multiprocessing import Process, Pipe
import numpy as np
The EnvWorker class inherits Process class and has the following attributes.
- env_name -> The name of the gym environment we are using, i.e. CartPole-v1.
- pipe -> This is a shared data structure which will be used to exchange information between the parent process and the EnvWorker object process.
- name -> A string to name the Process.
- NotDisplay -> A boolean value that is used to enable/disable simulation output of the environment.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class EnvWorker(Process):
def __init__(self, env_name, pipe, name=None,NotDisplay=False):
Process.__init__(self, name=name)
self.env = gym.make(env_name)
self.pipe = pipe
self.name = name
self.Display= not NotDisplay
print "Environment initialized. ", self.name
def run(self):
observation=self.env.reset()
param=self.pipe.recv()
episode_return=0
while True:
time.sleep(0.005)
decision=np.matmul(observation,param)
action=1 if decision>0 else 0
observation, reward, done, _ = self.env.step(action)
episode_return+=reward
self.env.render(close=self.Display)
if done:
self.pipe.send(episode_return)
episode_return=0
param=self.pipe.recv()
if param=="EXIT":
break
self.env.reset()
The run function is called when the EnvWorker instance process is executed. The process waits for the shared pipe to send param parameter, on receiving which it enters a while loop that repetitively computes an action for each observation of an episode of the environment and returns rewards through the pipe. When the episode ends (the pole falls or crosses the designated zone or completely balances the rod for 500 time steps), the done flag is set which causes the environment to reset itself and wait for the next param to start a new episode (or end episode if “EXIT” string is sent). Notice that param value that is sent through the pipe controls the action being taken for observations, and our problem is to find a param value that leads to better and better return for the episodes. We can now test this parallel implementation of the EnvWorker to run five consecutive episodes of CartPole-v1 environment as shown below.
1
2
3
4
5
6
7
8
9
p_start, p_end = Pipe()
env_worker = EnvWorker("CartPole-v1", p_end, name="Worker",NotDisplay=True)
env_worker.start()
for i in range(5):
p_start.send(np.random.uniform(-1,1,4))
episode_return = p_start.recv()
print "Reward for the episode ",i," ->", episode_return
p_start.send("EXIT")
env_worker.terminate()
Five episodes of the CartPole environment based on a random.
We now create a ParallelEnvironment class which has a collection of EnvWorker processes and is used to run iterations of the collection of processes based on a collection of param vectors (our flock of birds). The ParallelEnvironment class is shown below. The ParallelEnvironment class has the following attributes.
- env_name -> The name of the openAI gym environment i.e. CartPole-v1 in our case.
- num_env -> The number of parallel environments i.e. number of EnvWorker instances belonging to the class.
- NotDisplay -> Boolean value that enables/disables display of individual environments while training.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class ParallelEnvironment(object):
def __init__(self, env_name, num_env,NotDisplay):
assert num_env > 0, "Number of environments must be postive."
self.num_env = num_env
self.workers = []
self.pipes = []
for env_idx in range(num_env):
p_start, p_end = Pipe()
env_worker = EnvWorker(env_name, p_end, name="Worker"+str(env_idx),NotDisplay=NotDisplay)
env_worker.start()
self.workers.append(env_worker)
self.pipes.append(p_start)
def episode(self, params):
returns = []
for idx in range(self.num_env):
self.pipes[idx].send(params[idx])
for idx in range(self.num_env):
return_ = self.pipes[idx].recv()
returns.append(return_)
return returns
def __del__(self):
for idx in range(self.num_env):
self.pipes[idx].send("EXIT")
for worker in self.workers:
worker.terminate()
The init function simply initializes all the EnvWorker instances and sets up the pipes to communicate with those processes. The episode function receives a list params using which it runs an episode of each environment, and returns a corresponding list returns containing the net returns of every episode. The del function is used to kill all the EnvWorker processes after the work of the ParallelEnvironment class is done.
The Parallel environment is all set up and now lets implement the PSO to update the batch parameters. To do this we create an instance of ParallelEnviroment class and then call episode class function again and again with updated parameters (based on PSO update), until all the environments converge to maximum returns of the environment(i.e. 500 for CartPole-v1). The implementation is shown below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
num_envs = 10
NotDisplay=False
velocity_alpha=0.01
env_name="CartPole-v1"
p_env = ParallelEnvironment(env_name, num_envs,NotDisplay)
params=[]
best_params=[]
best_returns=[]
best_pos=0
velocity=[]
iter_cnt=0
inertia=1
cognitive=1
social=1
for i in range(num_envs):
params.append(np.random.uniform(-1,1,4))
best_returns.append(0)
best_params.append(np.array([0 for i in range(4)]))
velocity.append(np.array([0.0 for i in range(4)]))
while True:
returns=p_env.episode(params)
iter_cnt+=1
#Output of the batch episode.
print "Number of batch episodes ran -> ",iter_cnt
print "Parameter for the batch for last episode ->"
print np.around(params,3)
print "Best Parameters for the batch for all episodes ->"
print np.around(best_params,3)
print "Returns for the batch for last episode -> ",returns
print "Returns for the batch for all episodes -> ",best_returns
print "Rate of change of parameters for the batch -> "
print np.around(velocity,3)
#Exit condition
if returns==best_returns:
print "Batch converged after {} iterations.".format(iter_cnt)
p_env.__del__()
# Run a final episode using the average of all the final parameters
p_start, p_end = Pipe()
env_worker = EnvWorker("CartPole-v1", p_end, name="Worker",NotDisplay=True,delay=0.02)
env_worker.start()
p_start.send(np.sum(best_params,axis=0)/num_envs)
episode_return = p_start.recv()
print "Reward for the final episode ->", episode_return
p_start.send("EXIT")
env_worker.terminate()
# update according to PSO algorithm
for i in range(num_envs):
if(returns[i]>=best_returns[i]):
best_returns[i]=returns[i]
best_params[i]=params[i]
best_pos=returns.index(max(returns))
for i in range(num_envs):
velocity[i]=(inertia*velocity[i]
+cognitive*np.random.uniform(0,velocity_alpha)*(best_params[i]-params[i])
+social*np.random.uniform(0,velocity_alpha)*(best_params[best_pos]-params[i]))
params[i]+=velocity[i]
pass
A run of the above implementation of that converges after 64 batch iterations.
The final run that balances the pole perfectly.
The above implementation can be done using the Swarm class we created above, but for simplicity, it has been implemented without using the Swarm class. The PSO performs exceptionally well and converges after mere 64 iterations. On average, the number of iterations for convergence lies around 60-70, which is quite noteworthy.