


| Designed by Aaron Tan | Terms of Use © NUS 2010-2013 |
:
???
???
Chapter 1 Problem Solving
In this chapter you will learn about- The craft of problem solving, and the mental activities it entails.
- The need for creativity in problem solving, and some fallacies of creative thinking.
- What an algorithm is.
- The relationship between data and algorithm.
- The characteristics of an algorithm.
- Using pseudo-codes and flowcharts to represent algorithms.
1.1 Preliminaries
Problem-1: You are back from a leisure stroll in the park, and discover that you have dropped your wallet that is of great sentimental value to you. How do you retrieve your lost wallet?In our daily life, we encounter problems big and small. Some are easy to solve; some are tough nuts to crack. Some call for a structured solution; some require an unstructured approach. Some are interesting; some are not.
As for the nature of problems, they range from the mathematical to the philosophical. In computing, we deal with algorithmic problems whose solutions are expressed as algorithms.
You will learn more about algorithmic problem solving later. For the time being, we shall study problem solving in general. However, we still want to confine our domain within the logical applications of scientific and mathematical methods. Therefore, we will exclude problems such as "How long will the America government shutdown last?", "How to become a millionaire in 21 days?", "How to score straight A's in the examinations?" and "How many computer scientists does it take to change the light bulb?"
Returning to the wallet-in-the-park problem, have you found a solution?
If you have, then something is fishy. The problem statement is incomplete. Where did you actually drop the wallet? Did you assume that it was dropped at the park? Could it have happened on the way home? If the wallet was indeed dropped at the park, what is the park like?
These questions (and more, if you can think of) must be answered before you could reach a complete understanding of the problem. Assumptions should not be made without basis. Irrelevant information (such as the sentimental value of the wallet) should not get in the way. Incomplete information must be sought. You could only fully understand the problem after all ambiguities are removed. Only then should you set out to solve the problem.
Now, supposed your wallet was lost in the rectangular park 2km by 1km. How do you recover the wallet?

Problem-2: A square, where each side has length 2a, is inscribed in a circle. What is the area of the circle?
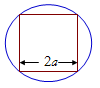
This is a simple, clearly stated problem on geometry. After you have obtained a full understanding of the problem, you need to devise a plan. You need to determine the input (the given datum – the length of each side of the square) and the output (the unknown – the area of the circle). You use suitable notation to represent the data, and you examine the relationship between the data and the unknown, which will often lead you to a solution. This may involve the calculation of some intermediate result, like the length of the diagonal of the square. You need to make use of the domain knowledge on basic geometry.
Problem-3: You are to ship a wolf, a sheep and a cabbage across the river. The boat can only hold the weight of two: you plus another item. You are the only one who can row the boat. The wolf must not be left with the sheep unsupervised, or the wolf will eat the sheep. Neither should the sheep be left alone with the cabbage. How do you fetch them over to the other side of the river?
This type of problem involves logic (and finds its place in a subject of computer science called logic programming, but I digress). The required solution is not a computed value as in Problem-2, but a series of moves that represent the transition from the initial state (in which all are on one side of the bank) to the final state (where all are on the opposite side).
Problem-4: The well-known Pascal's triangle is shown below.
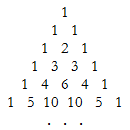
The extremities hold the 1's. For the rest, each value is the sum of the nearest two numbers above it, one on its right and the other on its left. How do you compute the combination nCk using the Pascal's triangle? How are the values related to the coefficients in the expansion of (x+y)n for non-negative n?
[The combination nCk, or n!/((n-k)!k!), is the number of possible ways of picking k items out of n items, without regard to order. Also denoted by C(n,k).]
Problem-5: Given a rectangular grid as shown below. You may move from one intersection to another, governed by the rule that you can travel only upwards or to the right, along the grid lines. How many paths are there from each of the intersections to the top-right corner of the grid? For example, there are two paths from point A to point C, one that goes right and then turns upwards, and the other that goes up and turns right.
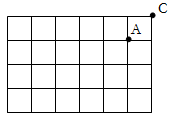
How is this problem related to the Pascal's triangle? Knowing the relation, how would you use Pascal's triangle to solve this problem?
This illustrates the oft-encountered situation that calls for relating a problem on hand to one that we have solved before. By consciously seeking out the similarity among problems, and performing problem transformation, these help us to sharpen our problem solving dexterity.
1.2 The Problem Solving Process
"A great discovery solves a great problem but there is a grain of discovery in the solution of any problem. Your problem may be modest; but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery. Such experiences at a susceptible age may create a taste for mental work and leave their imprint on mind and character for a lifetime."
– George Pólya
In his book, Pólya enumerates four phases a problem solver has to go through. First, we need to understand the problem, and clarify any doubts about the problem statement if necessary, as we have discussed in Problem-1. Second, we need to find the connection between the data and the unknown, to make out a plan for the solution. Auxiliary problems might be created in the process. Third, we are to carry out our plan, checking the validity of each step. Finally, we have to review the solution.
The four phases are outlined below. Note that asking questions is a running theme in all phases of the process. In fact, asking questions is part and parcel of learning (refer to the wheel of learning). As such, you should start cultivating an inquisitive mind today, if you have not done so.
- Phase 1: Understanding the problem.
- What is the unknown? What are the data?
- What is the condition? Is it possible to satisfy the condition? Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory?
- Draw a figure. Introduce suitable notation.
- Separate the various parts of the condition. Can you write them down?
- Phase 2: Devising a plan.
- Have you seen it before? Or have you seen the same problem in slightly different form?
- Do you know a related problem?
- Look at the unknown! Try to think of a familiar problem having the same or similar unknown.
- Split the problem into smaller, simpler sub-problems.
- If you cannot solve the proposed problem try to solve first some related problem. Or solve a more general problem. Or a special case of the problem. Or solve a part of the problem.
- Phase 3: Carrying out the plan.
- Carrying out your plan of the solution, check each step.
- Can you see clearly that the step is correct?
- Can you prove that it is correct?
- Phase 4: Looking back.
- Can you check the result?
- Can you derive the result differently?
- Can you use the result, or the method, for some other problem?
1.3 Creative Thinking
"Most new discoveries are suddenly-seen things that were always there. A new idea is a light that illuminates presences while simply had no form for us before the light fell on them."
– Susan Langer
The dissection on the problem solving process produces a finding that guides, not prescribes. It provides questions, not answers. It is a checklist, not a panacean device. Hence, the opportunities of solving problems do not cease with the revelation. In fact, this is just the beginning.
A rich knowledge base and effective techniques are requisites for problem solving. However, there appears to be another quality that makes some better problem solvers than others, though they may be equally knowledgeable. They call it creativity.
Many are intrigued by the ingenuity and creativity of prominent personalities the like of Thomas Edison, Van Gogh, and Albert Einstein, and hope to acquire this asset to apply it in problem solving. Creative thinking has become the buzzword these days. What exactly is creativity? Can it be taught? Here, we shall dispel some myths around creative thinking. The following pointers are found in the book "Creative Thinking & Problem Solving" [2].
- Myth 1: Creativity requires genius.
Get yourself or your mental straitjacket out of the way; believe in yourself and in the possibility of thinking more intuitively and creatively.
- Myth 2: You have to be odd to really turn on the imagination afterburners.
Creative thinking is sound, not strange, reasoning. To create, you must be mentally and emotionally flexible yet persistent enough to extract and recombine threads from daily experience, your knowledge and image bank, the senses, and intuition.
- Myth 3: Creative thinking isn't rigorous, but uses simple processes.
Real creative thinking takes practice and involves carefully following principles and effective techniques.
So you see, there is no big secret behind creative thinking. Creativity does not spurt out of a vacuum, but is the result of a concoction of knowing the principles, applying the right methods, plus sheer concentration and purposeful determination.
Another misperceived notion about creativity is that all constraints must be lifted before creativity can take reign. Often we heard students complain about restrictions imposed on their assignments, for example, the barring of certain methods in their solution. They charged that such a ban amounted to stifling their creativity. What they did not realise is that on the contrary, the best opportunities for creativity are such exacting times when the resources are limited or constrained. Creativity is not equivalent or tied to freedom.
Neither is creativity characterised by an absence of direction. When creative thinking is applied to problem solving, the mind wanders in search for ideas, of which some may be the wildest or the most unorthodox, but the objective has to stay in the back of the solver's mind. This reiterates the importance of understanding the problem, and it brings out the issue on problem definition.
The authors of the book "Strategies for Creative Problem Solving" [3] have this to say about the importance of producing correct problem definitions in handling real-life situations.
"Problem definition is a common but difficult task because true problems are often disguised in a variety of ways. It takes a skilful individual to analyse a situation and extract the real problem from a sea of information. Ill-defined or poorly posed problems can lead novice (and not so novice) engineers down the wrong path to a series of impossible or spurious solutions. Defining the 'real problem' is critical to finding a workable solution."
– H. Scott Fogler and Steven E. LeBlanc
Ill-defined problems may mislead the solver into diverting his attention to the wrong problems, as illustrated in a real-life case in the following article. (Article to be added later.)
1.4 Algorithms
Earlier, we expounded the working of problem solving from a general perspective. In computing, we focus on the type of problems categorically known as algorithmic problems, where their solutions are expressible in the form of algorithms.
An algorithm is a well-defined computational procedure consisting of a set of instructions, that takes some value or set of values, as input, and produces some value or set of values, as output. In other word, an algorithm is a procedure that accepts data, manipulate them following the prescribed steps, so as to eventually fill the required unknown with the desired value(s).
[The term algorithm was derived from the name of Mohammed al-Khowarizmi, a Persian mathematician in the ninth century. Al-Khowarizmi → Algorismus (in Latin) → Algorithm.]

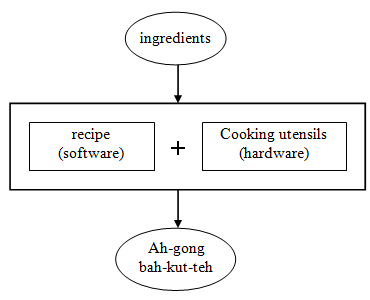
Tersely put, an algorithm, a jargon of computer specialists, is simply a procedure. People of different professions have their own form of procedure in their line of work, and they call it different names. A cook, for instance, follows a procedure commonly known as a recipe that converts the ingredients (input) into some culinary dish (output), after a certain number of steps.
An algorithm, whose characteristics will be discussed later, is a form that embeds the complete logic of the solution. Its formal written version is called a program, or code. Thus, algorithmic problem solving actually comes in two phases: derivation of an algorithm that solves the problem, and conversion of the algorithm into code. The latter, usually known as coding, is comparatively easier, since the logic is already present – it is just a matter of ensuring that the syntax rules of the programming language are adhered to. The first phase is what that stumbles most people, for two main reasons. Firstly, it challenges the mental faculties to search for the right solution, and secondly, it requires the ability to articulate the solution concisely into step-by-step instructions, a skill that is acquired only through lots of practice. Many people are able to make claims like "oh yes, I know how to solve it", but fall short when it comes to transferring the solution in their head onto paper.
Algorithms and their alter ego, programs, are the software. The machine that runs the programs is the hardware. Referring to the cook in our analogy again, his view can be depicted as follows:
The first documented algorithm is the famous Euclidean algorithm written by the Greek mathematician Euclid in 300 B.C. in his book Euclid's Elements, Book VII. It is rumoured that King Ptolemy, having looked through the Elements, hopefully asked Euclid if there were not a shorter way to geometry, to which Euclid severely answered: "In geometry there is no royal road!"
The modern Euclidean algorithm to compute GCD (greatest common divisor) of two integers, is often presented as followed.
- Let A and B be integers with A > B ≥ 0.
- If B = 0, then the gcd is A and the algorithm ends.
- Otherwise, find q and r such that
A = qB + r where 0 ≤ r < B
Note that we have 0 ≤ r < B < A and gcd(A,B) = gcd(B,r).
Replace A by B, and B by r. Go to step 2.
Walk through this algorithm with some sets of values.
1.5 Data Types And Data Structures
In algorithmic problem solving, we deal with objects. Objects are data manipulated by the algorithm. To a cook, the objects are the various types of vegetables, meat and sauce. In algorithms, the data are numbers, words, lists, files, and so on. In solving a geometry problem, the data can be the length of a rectangle, the area of a circle, etc. Algorithm provides the logic; data provide the values. They go hand in hand. Hence, we have this great truth:
Data structures refer to the types of data used and how the data are organised in the program. Data come in different forms and types. Most programming languages provides simple data types such as integers, real numbers and characters, and more complex data structures such as arrays, records and files which are collections of data.
Because algorithm manipulates data, we need to store the data objects into variables, and give these variables names for reference. For example, in mathematics, we call the area of a circle A, and express A in terms of the radius r. (In programming, in general we would use more telling variable names such as area and radius instead of A and r, for the sake of readability.) When the program is run, each variable occupies some memory location(s), whose size depends on the data type of the variable, to hold its value.
1.6 Characteristics Of An Algorithm
What makes an algorithm an algorithm? There are four essential properties of an algorithm.
- Each step of an algorithm must be exact.
This goes without saying. An algorithm must be precisely and unambiguously described, so that there remains no uncertainty. An instruction that says "shuffle the deck of card" may make sense to some of us, but the machine will not have a clue on how to execute it, unless the detail steps are described. An instruction that says "lift the restriction" will cause much puzzlement even to the human readers.
- An algorithm must terminate.
The ultimate purpose of an algorithm is to solve a problem. If the program does not stop when executed, we will not be able to get any result from it. Therefore, an algorithm must contain a finite number of steps in its execution. Note that an algorithm that merely contains a finite number of steps may not terminate during execution, due to the presence of infinite loop.
- An algorithm must be effective.
Again, this goes without saying. An algorithm must provide the correct answer to the problem.
- An algorithm must be general.
This means that it must solve every instance of the problem. For example, a program that computes the area of a rectangle should work on all possible dimensions of the rectangle, within the limits of the programming language and the machine.
An algorithm should also emphasise on the whats, and not the hows, leaving the details for the implementation (i.e. program). However, this point is more apparent in more complicated algorithms at advanced level, which we are unlikely to encounter yet.
1.7 Pseudo-Codes And Flowcharts
We usually present algorithms in the form of some pseudo-code, which is normally a mixture of English statements, some mathematical notations, and selected keywords from a programming language. There is no standard convention for writing pseudo-code; each author may have his own style, as long as clarity is ensured.
Below are two versions of the same algorithm, one is written mainly in English, and the other in pseudo-code. The problem concerned is to find the minimum, maximum, and average of a list of numbers. Make a comparison.
Algorithm version 1:
First, you initialise sum to zero, min to a very big number, and max to a very small number.
Then, you enter the numbers, one by one.
For each number that you have entered, assign it to num and add it to the sum.
At the same time, you compare num with min, if num is smaller than min, let min be num instead.
Similarly, you compare num with max, if num is larger than max, let max be num instead.
After all the numbers have been entered, you divide sum by the numbers of items entered, and let ave be this result.
End of algorithm.
Algorithm version 2:
sum ← count ← 0 { sum = sum of numbers; count = how many numbers are entered? }
min ← ? { min to hold the smallest value eventually }
max ← ? { max to hold the largest value eventually }
for each num entered,
increment countave ← sum/count
sum ← sum + num
if num < min then min ← num
if num > max then max ← num
Note the use of indentation and symbols in the second version. What should min and max be initialised with?
Algorithms may also be represented by diagrams. One popular diagrammatic method is the flowchart, which consists of terminator boxes, process boxes, and decision boxes, with flows of logic indicated by arrows.
The flowchart below depicts the same logic as the algorithms above.

Whether you use the pseudo-code or the flowchart to represent your algorithm, remember to walk through it with some sets of data to check that the algorithm works.
1.8 Control Structures
The pseudo-code and flowchart in the previous section illustrate the three types of control structures. They are:
- Sequence
- Branching (Selection)
- Loop (Repetition)
These three control structures are sufficient for all purposes. The sequence is exemplified by sequence of statements place one after the other – the one above or before another gets executed first. In flowcharts, sequence of statements is usually contained in the rectangular process box.
The branch refers to a binary decision based on some condition. If the condition is true, one of the two branches is explored; if the condition is false, the other alternative is taken. This is usually represented by the 'if-then' construct in pseudo-codes and programs. In flowcharts, this is represented by the diamond-shaped decision box. This structure is also known as the selection structure.
The loop allows a statement or a sequence of statements to be repeatedly executed based on some loop condition. It is represented by the 'while' and 'for' constructs in most programming languages, for unbounded loops and bounded loops respectively. (Unbounded loops refer to those whose number of iterations depends on the eventuality that the termination condition is satisfied; bounded loops refer to those whose number of iterations is known before-hand.) In the flowcharts, a back arrow hints the presence of a loop. A trip around the loop is known as iteration. You must ensure that the condition for the termination of the looping must be satisfied after some finite number of iterations, otherwise it ends up as an infinite loop, a common mistake made by inexperienced programmers. The loop is also known as the repetition structure.
Combining the use of these control structures, for example, a loop within a loop (nested loops), a branch within another branch (nested if), a branch within a loop, a loop within a branch, and so forth, is not uncommon. Complex algorithms may have more complicated logic structure and deep level of nesting, in which case it is best to demarcate parts of the algorithm as separate smaller modules. Beginners must train themselves to be proficient in using and combining control structures appropriately, and go through the trouble of tracing through the algorithm before they convert it into code.
References
[1] Pólya, George, How To Solve It: A New Aspect of Mathematical Method, Princeton University Press, 2nd edition, 1988.
[2] Fabian, John P., Creative Thinking & Problem Solving, Lewis Publishers, 1990.
[3] H. Scott Fogler, and Steven E. LeBlanc, Strategies for Creative Problem-Solving, Prentice Hall, 1995.
10 October 2013