This lab assignment comprises three exercises. Only the first two exercises are graded, but you are strongly encouraged to attempt the third exercise.
You are advised to review the material covered in chapters 1 through 10 and read Programming Style, Design and Marking Guidelines before attempting this lab assignment. You should not use syntax or constructs not covered in lectures; you shouldn't need to and may even be penalized for doing so (if the objective of the assignment is undermined).
A word of advice: Code incrementally. Don't try to finish all parts of a program then compile it. Write your program in bits and pieces and compile frequently. Try to maintain a compilable program even while you are working on it. Submitting a compilable program that partially works is better than submitting an un-compilable one. This last point especially applies to the programming exams. Seriously, code incrementally.
The following topics have not been covered and hence you should not use them (if you are in doubt whether you can use certain features not mentioned below and are not yet covered in class, please consult your discussion leader or lecturer first):
You may assume that all input data are correct.
You should use Scanner class on System.in for input and System.out for output in your programs, unless otherwise stated.
Your last output statement should be a println and not print.
Test your programs thoroughly with your own input data before you submit to CourseMarker. Do not use CourseMarker as a debugging tool. For this lab, the number of submissions is set to 6. Only your last submission will be graded.
In general, the expected time to complete a lab assignment (including all graded exercises) is between 3 to 5 hours. You should aim not to spend more than 5 hours. It might be difficult at first, but it should get easier as you gain experience. Make that your target.
Sudoku is a popular logic-based number placement puzzle. The 9×9 board has 9 rows, 9 columns and 9 sections of 3×3 cells. The objective is to fill the board so that each row, each column and each section contains the digits from 1 to 9.
The puzzle is given as an incomplete Sudoku board in which some cells are blanks. The solver needs to fill in all the blank cells with the correct values.
Figure 1 below, taken from Wikipedia: Sudoku, shows a Sudoku puzzle and its solution.
There are numerous websites on Sudoku. Surf the Internet to explore!

Figure 1. A Sudoku puzzle and its solution.
You are given the following codes:
You are to write two programs Sudoku.java and PlaySudoku.java.
The class Sudoku defines a Sudoku puzzle, using a two-dimensional 9×9 integer array as its data member. You are to complete the following methods:
You may include additional methods to make your program more modular.
The method solve() uses this very simple algorithm:
Repeat the following until no more blank cells can be filled:
Scan the board from top to bottom, and for each row from left to right.
For each blank cell encountered:Examine the row, column and section the blank cell is in,
if only one value for that blank cell fits, fill it with that value.
Look at Figure 2 below for an example. Scanning the board from top to bottom, left to right, we encounter the first blank cell at A. After examining the row, column and section A is in, we conclude that it must be filled with the value 6.
Next is the blank cell at B. Since there can be two candidate values, the algorithm cannot fill in B yet.
Next we visit the blank cell at C, since the only value that fits is 5, we fill C with 5. And we continue with the rest of the board.
When we return to B in the next round, we will be able to fill it with the value 8.

Figure 2. An example on how the algorithm works.
Note that this algorithm solves only the simplest puzzles. For more difficult puzzles, it does not fill in all blank cells. Leave it as it is.
(You are not required to submit a solver that solves all Sudoku puzzles. This is beyond CS1101 and might be too tough to be done in two hours. Although some students have commented that the lab assignments are too easy, I wouldn't want to scare off the others. Hence, I shall leave this as an optional exercise for those who are interested, and you can present your solution at your discussion session. The ambitious ones may even turn this into a complete graphics-based Sudoku game!)
The toString() method returns a string representation of the Sudoku board. A blank cell is indicated as '-' in the string representation. See the second sample run below for an example.
PlaySudoku.java is an application program on the Sudoku class. Study the given partial code and complete the readBoard(Scanner) method.
The sample runs below show the user's inputs. 81 values are entered by the user, with 0 (zero) representing a blank cell.
(If you are programming in your sunfire UNIX account, or using line commands, you may simplify the data entry by creating a text file that contains the input data, then use the input redirection "<" to feed the data into your program. For example, create a text file sudoku.in that contains the 81 input values, and then type java PlaySudoku < sudoku.in to run the program.)
Sample run using interactive input (user's input shown in blue; output shown in bold purple):
$ javac Sudoku.java $ javac PlaySudoku.java $ java PlaySudoku Enter the board, using 0 to indicate a blank cell: 5 3 0 0 7 0 0 0 0 6 0 0 1 9 5 0 0 0 0 9 8 0 0 0 0 6 0 8 0 0 0 6 0 0 0 3 4 0 0 8 0 3 0 0 1 7 0 0 0 2 0 0 0 6 0 6 0 0 0 0 2 8 0 0 0 0 4 1 9 0 0 5 0 0 0 0 8 0 0 7 9 The Sudoku board solved: 5 3 4 6 7 8 9 1 2 6 7 2 1 9 5 3 4 8 1 9 8 3 4 2 5 6 7 8 5 9 7 6 1 4 2 3 4 2 6 8 5 3 7 9 1 7 1 3 9 2 4 8 5 6 9 6 1 5 3 7 2 8 4 2 8 7 4 1 9 6 3 5 3 4 5 2 8 6 1 7 9
Another sample run, showing a case where the puzzle cannot be solved completely by the given algorithm.
$ java PlaySudoku Enter the board, using 0 to indicate a blank cell: 4 1 9 0 0 0 7 2 0 0 0 0 0 0 9 3 4 0 5 0 0 0 0 0 6 0 0 9 0 0 4 8 6 0 0 0 0 0 8 0 9 0 1 0 0 0 0 0 2 1 3 0 0 9 0 0 6 0 0 0 0 0 7 0 8 2 6 0 0 0 0 0 0 9 4 0 0 0 8 6 3 The Sudoku board solved: 4 1 9 - - - 7 2 - 8 6 7 - - 9 3 4 - 5 2 3 - - - 6 - - 9 3 1 4 8 6 - - - 2 4 8 - 9 - 1 - - 6 7 5 2 1 3 4 8 9 - 5 6 - - - - - 7 - 8 2 6 - - - - - - 9 4 - - - 8 6 3
Submit your programs Sudoku.java and PlaySudoku.java through CourseMarker.
This is one of past year's CS1101X Practical Exam questions. The time limit given was 1 hour, so you should aim to complete it within an hour.
A bunny can hop at most 50 centimetres far. It wants to cross to the other side of the river, but it cannot swim. So the only hope is to hop on the rocks on the river, which are positioned in a straight line. The positions of the rocks are measured from the start location, assuming that the bunny starts at location zero. The opposite bank could be treated as a big rock.
In Figure 3 below, the rocks are at locations 32, 46, 70, 85, 96, 123, and the opposite riverbank at location 145.
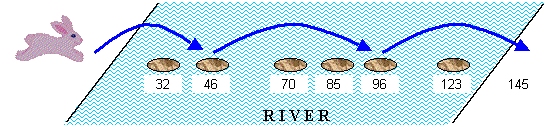
Figure 3. Positions of rocks.
The bunny will jump as far as it could for each hop. What is the smallest number of jumps it needs to take to reach the other side of the river? For the above example, it needs to make 3 jumps, as shown in the diagram above.
Write a program RabbitJumps.java that reads in a positive integer n that represents the number of rocks (including the opposite riverbank), and then on the next line n distinct positive integers in increasing order that represent the locations of the rocks. Your program should output the minimum number of jumps needed, or -1 if it is not possible for the bunny to reach the other side of the river.
To make your program more modular, you should include a method int countJumps(int[]) to compute the number of jumps required.
Sample run using interactive input (user's input shown in blue; output shown in bold purple):
$ javac RabbitJumps.java $ java RabbitJumps Enter n: 7 32 46 70 85 96 123 145 3
Sample run #2:
$ java RabbitJumps Enter n: 5 40 70 150 160 180 -1
Sample run #3:
$ java RabbitJumps Enter n: 11 30 70 75 120 160 170 180 190 200 246 258 7
Submit your program RabbitJumps.java through CourseMarker.
Note: Although this exercise is not graded, you are strongly encouraged to attempt it for practice, as it involves array of objects.
You are to write a program MyPolygon.java, which uses the pre-defined Point class. A Point object is a 2D point with integer x- and y-coordinates. Refer to Java API: java.awt.Point for details.
The class MyPolygon defines a simple polygon with a list of vertices, listed in clockwise or counter-clockwise direction. (A simple polygon is a polygon in which the only place two edges can meet is a vertex. Such a polygon has a well defined interior and exterior.)
The class MyPolygon contains the following data members:
(Compare this with the predefined class Java API: java.awt.Polygon.)
The class MyPolygon contains the following methods:
You may assume that no three consecutive vertices are co-linear.
Convex polygon
A polygon is convex if it contains all line segments connecting any pair of its vertices. A polygon that is not convex is a concave polygon. Figure 4(a) below shows a convex polygon and Figure 4(b) shows a concave one.
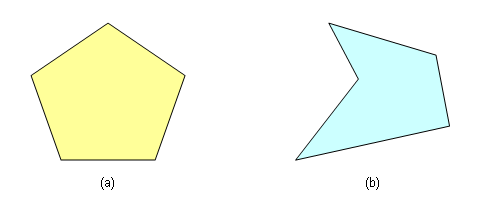
Figure 4. (a) A convex polygon. (b) A concave polygon.
A simple way to determine whether a polygon is convex is to conduct a walk along the boundary of the polygon, going from one vertex to the next. If we walk in the clockwise direction, as shown in Figure 5(a) below, then every turn is a right turn. For example, A-B-C is a right turn, so is B-C-D, and so on.
On the other hand, if we walk in the counter-clockwise direction, as shown in Figure 5(b) below, then every turn is a left turn.
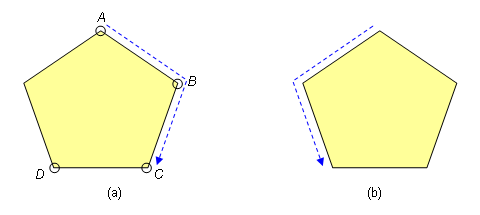
Figure 5. (a) Walking along the boundary of a convex polygon in a clockwise direction, every turn is a right turn. (b) In the counter-clockwise direction, every turn is a left turn.
As expected, a concave polygon will have a mix of right turn(s) and left turn(s).
Given three consecutive vertices A, B, and C of a polygon, to determine if A-B-C is a right turn or a left turn, we compute the determinant of this 3×3 matrix:

where A = (xA, yA), B = (xB, yB), and C = (xC, yC). If the determinant is a negative value, then A-B-C is a right turn; if the determinant is positive, then it is a left turn.
The determinant of a general 3×3 matrix is computed as follows:
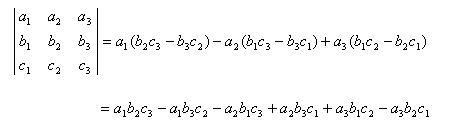
Sample run using interactive input (user's input shown in blue; output shown in bold purple):
$ javac MyPolygon.java $ java MyPolygon Enter number of vertices: 5 Enter vertices: 0 10 5 20 10 10 8 0 2 0 Polygon = [ (0,10) (5,20) (10,10) (8,0) (2,0) ] Area of bounding box = 200 Convex
Another sample run:
$ java MyPolygon Enter number of vertices: 4 Enter vertices: 0 0 -6 -2 4 -2 0 5 Polygon = [ (0,0) (-6,-2) (4,-2) (0,5) ] Area of bounding box = 70 Concave
Submit your program MyPolygon.java through CourseMarker.
The deadline for handing in all programs is 24 October 2007, Wednesday, 23:59. Late submissions will NOT be accepted.
Start early. Do not wait till the eleventh hour and rush to meet the deadline.