Problem Set 1: Welcome to CS3217!
Issue Date: Monday, 13 January 2020
Due Date: Sunday, 19 January 2020
Total points: 50 points
Reminder:
- Please read the entire problem set before starting!
- Start early! Many of your seniors have regretted not starting early. Even week 1 is not chill for CS3217!
Introduction
In this problem set, we are going to implement the Graph Abstract Data Type (ADT). This ADT will primarily be used to implement breadth-first search (BFS) and depth-first search (DFS) -- imagine, for example, that clients of the Graph ADT will use it as part of a larger maze navigation program. You should therefore ensure that the ADT is optimised to run these algorithms efficiently, in terms of both time and space.
If you need a refresher on how these algorithms work, please consult resources on the internet, such as VisuAlgo.
Getting Started with Swift
If you did not attempt Problem Set 0, please quickly get up to speed on Swift and iOS development. As mentioned on the PS0 page, Apple has provided extensive documentation on Swift and iOS development (it is in their best interest to do so). In the spirit of not reinventing the wheel, you are encouraged to refer to them, which we have linked to on the tips page.
Definitions and Terminology
A graph is a collection of nodes (also called vertices) and edges. Each
edge connects two nodes. In a directed graph, edges are one-way: an edge
e = (A, B) indicates that a node, B is directly reachable from another node,
A. To indicate that B is directly reachable from A and vice-versa, a directed
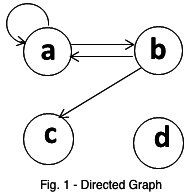
graph would have edges (A, B) and (B, A). Fig. 1 below is an example of a
directed graph.
On the other hand, in an undirected graph, we can travel in either direction along the edges between nodes.
A node A is said to be adjacent to a node B if there exists an edge connecting A to B. In Fig. 1 below, the neighbours of A are A and B.
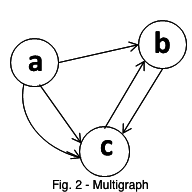
In a multigraph, there can be any number of edges (zero, one, or more) between a pair of nodes. Fig. 2 below shows a multigraph with 2 edges from A to C. In this assignment, a graph cannot contain more than one edge with the same weight between a pair of nodes.
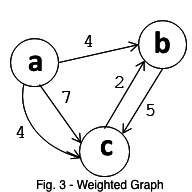
In a weighted graph, such as in Fig. 3 below, every edge has a weight associated with it.
Specifications
The purpose of a specification is to document a program's logic, the range of inputs that it can safely operate on, and its expected behaviour. Interpreting an ADT involves understanding its specifications - what it does and does not. So for ADTs, the specification describes what this ADT represents, its purpose, its representation invariant, and the behaviour of each of its methods. At the start of the ADT, the specification gives a summary of the ADT, mainly the abstraction function and the representation invariant. The abstraction function is a mapping from the state of an ADT instance to some mathematical object that it represents. The representation invariant is some condition that all valid instances of the ADT must satisfy, which is essentially the format of the ADT. Above the code for each method, there are comments describing its behaviour, expected input and output. The comments will follow Apple-specific markup format, which can be referenced here.
Through this problem set, you will practice interpreting and implementing specifications of some ADTs, and gain a better appreciation of the role that fundamental tools such as object models and representation invariants play in the design of a module.
Part 1: The Stack and Queue ADTs (10 points)
Since BFS and DFS uses queues and stacks respectively, we shall start by implementing these ADTs.
- A skeleton for both the Stack and the Queue ADTs have been provided in
Stack.swiftandQueue.swiftrespectively. Implement both ADTs by filling up the method implementations according to the descriptions. (7 points) - After you have implemented the ADTs, please write tests to ensure that your
implementation is correct. Make sure that your tests are extensive, and cover
all possible edge cases. Create new
StackTests.swiftandQueueTests.swiftfiles for your tests. (3 points)
Notes
You may adapt the type and the method signatures provided in the skeleton given if you wish. For example, you may change the type of the ADTs (into enum/struct/class), or you may modify methods to return optionals / throw exceptions. However, you may not change the behavior of the happy path use case (e.g. if a stack contains an item,
peekandpopshould still peek or pop the top item in the stack).If you do change them, please document and justify your changes in the
README.mdfile. Marks may be deducted for unreasonable changes or bad justification.Note that you are allowed to do this since we assume that only the Graph ADT is the client of the Stack and Queue ADTs you just implemented. If these ADTs are used by other people, care must be taken to ensure backwards compatibility.
Please make sure that your ADTs perform optimally. Marks will be deducted for bad performance.
Part 2: Implementing the Graph ADT (21 points)
The project that you are given contains two ADTs:
Node, representing nodes of the graphEdge, representing edges of the graph
Please check these code, located in Node.swift and Edge.swift. Again, you
may adapt these ADTs as you wish, since the Graph ADT is the only client of
this code. Please document and justify your changes if you do.
Now that you have seen these ADTs, implement the Graph ADT provided in
Graph.swift. Specifications have been written at the top of the functions
you need to implement. If you do adapt this Graph ADT, document and justify
your changes. (16 points)
In addition, please answer the following questions in your README.md file.
You are given the private function
checkRepresentationinside theGraphclass. This function is supposed to check if the representation invariants of the ADT is fulfilled or not. The way it is meant to used is to putassert(checkRepresentation())inside the methods so that the representation invariants is not violated. For an example of this, you may refer to
Edge.swift.Here, you have several choices. You may choose to implement this function and use this to assert the representation invariants of your implementation; if you do so, justify where you put the assertions, and why you put them. For example, you might want to put it at the beginning of constructors; at the end of constructors; at the beginning of methods; at the end of methods; or some other place, or even some combination of these. Justify why you decided to put (or not) the assertions at these places.
Alternatively, you can choose to discard this function; if you do so, justify why you decided to not use
checkRepresentationin your class. (2 points)There are several ways to represent a graph. Here are a few:
- As a collection of edges
- As an adjacency list, in which each node is associated with a list of its outgoing edges.
- As an adjacency matrix, which explicitly represents for every pair (A, B) of edges, whether there is an edge from A to B, and how many.
Briefly discuss the advantages and disadvantages of each of these three ways. Afterwards, describe and justify the Graph representation you choose to implement. (2 points)
Imagine that the original representation invariant was changed to include a new requirement that there can be at most 1 edge between a source and destination node. Which method or constructor implementations would have to change? Please list them. For each changed piece of code, describe the changes informally, and indicate how much more or less complex (in terms of code clarity and/or execution efficiency) the result would be. Note that the new implementations must still adhere to the given spec. (1 point)
Part 3: Testing your Graph Implementation (5 points)
Similar to Stack and Queue, write tests for your Graph ADT to ensure that your implementation is correct.
Part 4: Using Trees for Cryptography (14 points)
In this problem, you are going to use a tree to encrypt and decrypt strings. The encrypt and decrypt functions are defined as follows:
- Encrypt: perform string-to-tree with breadth-first order and then tree-to-string with depth-first order
- Decrypt: perform string-to-tree with depth-first order and then tree-to-string with breadth-first order
In order to perform the string-to-tree conversions, you will be provided with a key, which is an integer value greater than 1. This key specifies the number of children for every letter in the string (or the number of children of each node in the intermediate tree). The intermediate tree is a perfect tree, which means that:
- Every node other than the leaves has exactly k children.
- All leaves have the same depth.
For example, consider the string HELLO WORLD. When performing the encrypt
operation with the key as 2, the breadth-first string-to-tree conversion
would result in the following tree:
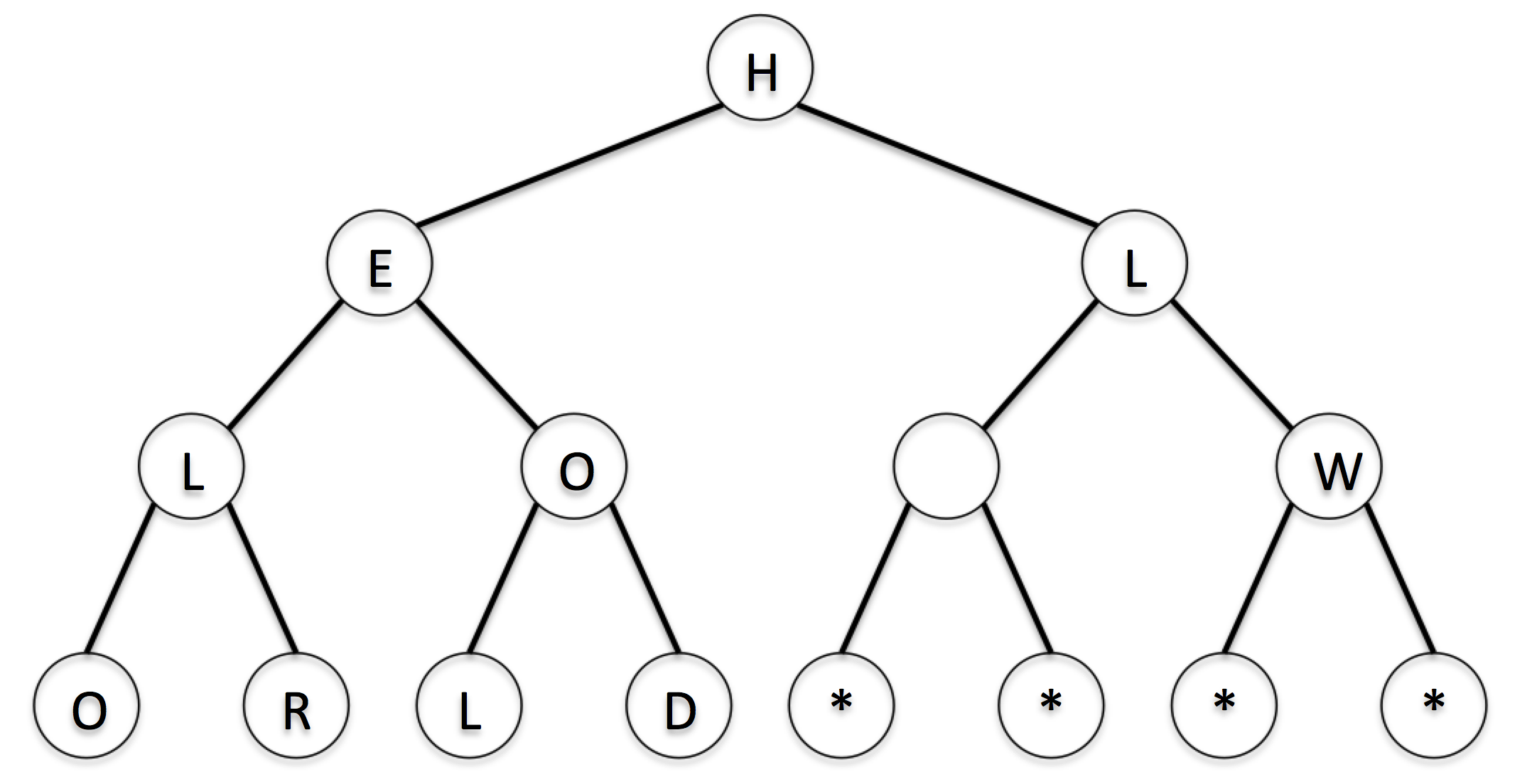
In order to create a complete binary tree, we need to append some extra nodes
with a string label * to the end of the tree to conform to the key. You can
assume that the input string has no * character. (Note that the empty node
in the diagram represents the space in the original string.)
In the second part of the encrypt operation, this tree is converted to a string
using the depth-first approach. This would result in the following string:
HELOROLDL **W. Note that the special characters must be removed if they
appear at the end of the string after the conversion.
In addition, the depth-first approach should traverse the tree such that among nodes in the same level, the node that is traversed first is the one that is created first when doing the string-to-tree conversion. This means that if the string-to-tree conversion creates the tree left to right, the tree-to-string conversion should traverse left to right as well.
If this resultant string is used as the input for the decrypt operation using
the same key, it should give back the initial string i.e. HELLO WORLD.
Now, follow the steps described below to implement the encrypt/decrypt functionalities:
First, you must design and implement a
TreeADT inTree.swift. You should provide a suitable specification for the ADT and also define the representation invariant properly. Please write this specification at top of theTreeobject, in the style of e.g.Graph.swift.You may extend the
GraphADT created in the previous problem or use a different representation for theTree. YourTreeADT should be a generic one that is reusable outside of this question, and should support common data structure operations, for example, insertion and deletion. You may add new files to the project to support your implementation; however, you are required to mention them inREADME.md. (5 points)Implement a class extension for
TreeinTree+Traversal.swift. The specifications for the class extension can be found within the skeleton provided. (3 points)Implement a class extension for
StringinString+Cryptography.swift. The specifications for the class extension can be found within the skeleton provided. (3 points)For the problem(s) above, take note that your algorithm(s) will need to append extra nodes to the end of the tree such that it will satisfy the perfect tree requirement. Likewise, extra nodes appended in the tree must also be dealt with appropriately: they should not appear at the end of the converted string.
Write appropriate test cases in
TreeTests.swiftandString+CryptographyTests.swiftto test theTreeADT and the encrypt and decrypt functionalities. Keep in mind that given a string, performing the encrypt operation followed by the decrypt operation using the same key should produce the same string. (3 points)
Bonus: Code Review (5 points)
Note: This section is entirely optional.
Deadline: Wednesday, 22 January 2019
Writing code is very different from reading code. While a chunk of code may be obvious to you when you are writing it, it may look cryptic to someone who is reading your code for the first time.
Hence, for this task, we will give you the chance to look at and review another student's code. A partner will be assigned to you, whose Problem Set 1 you will review. We will open up access to your partner's repository after your partner has submitted Problem Set 1.
For this, a separate branch called peer-review will be created on your
partner's repository. Use this branch to comment on your partner's code. Once
you are done, submit a pull request to the master branch.
There are two ways you can give comments:
- Inline comments, where you write comments on top of the relevant lines of code that you think can be improved or you feel is interesting / impressive.
- General comments that you can put in the pull request body, when you submit
the pull request to the
masterbranch.
Here are some things that you can comment on, as well as suggest improvements:
- Code style and structure
- General design
- Alternative code style that you used in your PS submission
- If any part of the code looks interesting
- New tricks / techniques that you have learnt from reading the code
You will get full marks if you put in effort, and 1 point if we think that you put in barely any effort. (If your partner's code is perfect and you can't find anything wrong, you can discuss alternative designs or things you have learnt from the code!)
Bonus: Reflection (3 points)
Answer the reflection questions in this form for 3 bonus points!
