Weekly Report 4
From: Chen Guoyi
Sent: Sunday, February 25, 2024 11:39 PM
To: Prahlad Vadakkepat; Liang Yuanchang
Cc: Chen Guoyi
Subject: [UROP] Weekly Report 4 - Game
|
Dear Professor Vadakkepat,
I hope this email finds you well.
As indicated in the subject of this email, I developed a game last week, but it is more than just a game; it has the potential to be an innovative component of our UROP project. This online game, named "AI Training Game for Autonomous Robot in Complex Interactive Environment," is based on JavaScript code and allows players to play through a browser. Its mission is to collect control data from human players, thereby facilitating the training of our UROP project robot using algorithms such as reinforcement learning.
The game's algorithm design is based on my [UROP] Weekly Report 1 and 2. The game will use the artificial potential field (APF) method from the first week to construct an inertial reference system, and the robot's motion equation is built through the affine function designed in the second week. In the game, human players will control the robot to avoid obstacles while moving towards a target on a large map. To simulate the robot's SLAM vision, human players can only see a very small range of the environment. To achieve affine control, humans interact with the robot through the mouse, generating acceleration in the direction of the mouse (like the escape force); the farther the mouse is from the robot, the greater the acceleration.
The game will record kinematic data of the robot and the environment, including time, position, velocity, actual acceleration, expected acceleration, relative speed with the nearest obstacle, and distance to the target, among others. I will use these data to analyze how humans make safe control strategies and path planning, thereby designing a safety control algorithm based on reinforcement learning. If feasible, in the conclusion of the paper, I will compare the performance of humans with that of our robot trained in the ROS environment, thus arguing for the effectiveness of the Redesign proposition in our UROP proposal.
The game underwent internal testing today with my friends, and we mathematically proved the effectiveness of the virtual physical environment we constructed. If you have time, I hope you can also experience and test the game using a laptop (not phone or iPad!).
The game link and guide are available at https://www.comp.nus.edu.sg/~guoyi/project/urop/training/.
Today is the Lantern Festival of China, marking the official end of the Chinese New Year and the beginning of spring for the new year. I wish you and your family good health and smooth work in 2024!
I hope you have a nice week ahead!
Best regards,
Guoyi
Weekly Report 3
From: Chen Guoyi
Sent: Sunday, February 18, 2024 5:01 PM
To: Prahlad Vadakkepat; Liang Yuanchang
Cc: Chen Guoyi
Subject: [UROP] Weekly Report 3 - Baseline Study Finished
|
Dear Professor Vadakkepat,
I hope this email finds you well.
I am writing to summarize my work from the past week and outline my plans for the upcoming weeks. Following the guidelines, I have been progressing as scheduled. I presented last week's work to Mr. Liang during our routine weekly group meeting this Wednesday, where I received valuable feedback and support.
Last week, I completed a baseline study on safety control through CMU's E-lecture 16-883: Provably Safe Robotics (Spring 2023). This PhD-level course from CMU's Computer Science department covers the latest theories on ensuring the safety of autonomous systems, emphasizing the importance of accurate system operations across perception, decision-making, and control. It discusses strategies like planning, prediction, learning, control, neural network verification, and analysis of closed-loop and multi-agent systems.
I've compiled LaTeX notes [attached in this email: baseline_study_v0217.pdf] on this study, focusing on the instructor's research and application of safety control theories. I intend to reference the course's recommended papers directly in future work. The notes outline the application of safe control theory in complex human-robot interactions. I paused the note at the closed-loop systems section because I planned a further refinement on robot locomotion constraints next week (I will review Prof. Chew Chee Meng's feedback control course and ME3243 and redesign the affine system constraint for better performance in the industrial environment simulation as stated in my UROP proposal).
There's a connection to our previous discussions in Week 2, specifically relating to your EAPF paper and optimizing escape force methodology in safety control. I look forward to exploring how these ideas might enhance your EAPF method.
Apologies for the delay in this week's feedback; the course content required extra attention. I plan to provide next week's update before next Saturday afternoon.
Thank you and Mr. Liang for your guidance and support! I hope you have a great week ahead.
Best regards,
Guoyi
Appendix: Notes
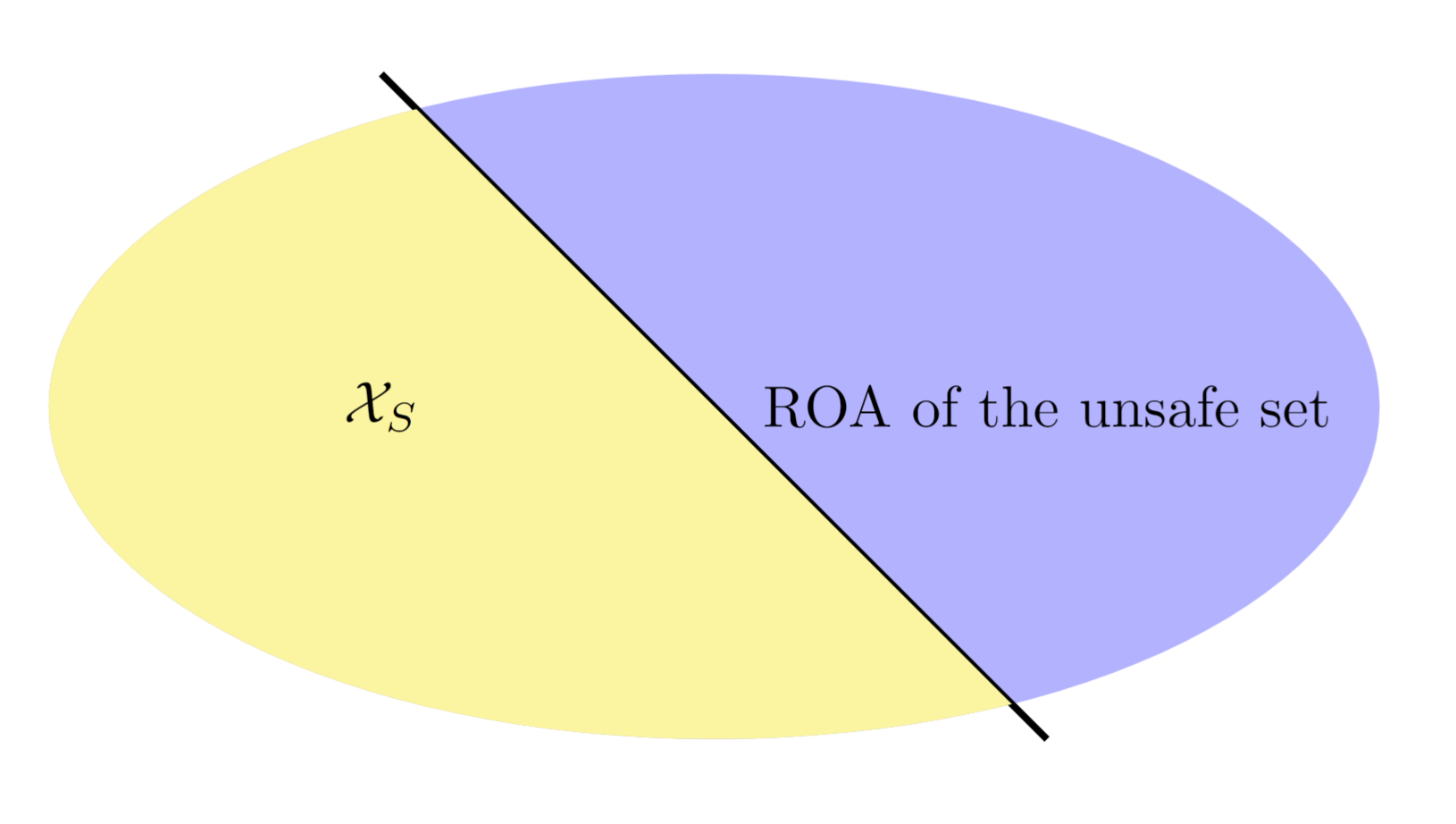
Regions of Attraction (ROA)
Because of the existence of the Regions of Attraction (ROA), the
naive safe strategy is unsafe in some dynamic situations. We define the
naive safe set as \(\mathcal{X}_S\),
and the relationship between \(\mathcal{X}_S\)
and ROA is shown below:
Safety Index
We define a safety index function \(\phi\), which is: \(\phi = \xi \mapsto \mathbb{R}\). A negative
value of safety index \(\phi\) will be
assigned when the state of the robot (\(\xi\)) is unsafe. Otherwise, the value of
\(\phi\) should be positive. The
expression shows the relation between ROA and the \(\mathcal{X}_S\): \(\{\xi:\phi(\xi)\leq0\}\subseteq
\mathcal{X}_S\). The new expression of naive safe strategy by
using the safety index is: \[\phi_0=d^2_{min}-d^2\]
where:
By considering the ROA, we need to consider the relative speed
between robots and humans; the improved version of the safety strategy
in high-level safe control by using the safety index is:
\[\phi = d^2_{min}-d^2+k \cdot \dot{d} =
\phi_0 + k \cdot \dot{\phi}_0\]
where:
Design Safety Index
The basic idea of this safety index for safe control in one human and
robot interaction environment has been proved by Dr. Liu C. in DSCC 2014
(DOI: 10.1115/DSCC2014-6048). The theory has been retrieved from her
previous work:
Theorem: For \(\mathcal{X}_S=\{\xi: \phi_0(\xi) \leq 0
\}\), define: \(\phi = \phi_0 + k_1
\cdot \dot{\phi}_0+\cdots+k_n\phi_o^{(n)}\). Then the set \(\{\xi:\phi(\xi) \leq 0\} \cap
\mathcal{X}_S\) is forward invariant if \(\dot{\phi}(\xi) \leq 0, \forall \xi \in
\{\xi:\phi(\xi)=0\}\) and globally attractive if \(\dot{\phi}(\xi) \leq - \eta, \forall \xi \in
\{\xi:\phi(\xi) > 0\}\).
Safety Index Control
Strategy
Hence, we can conclude a safe control strategy based on the safety
index:
-
No extra safe control required when: \(\xi\in\{\xi:\phi(\xi)<0\}\).
-
Forward in-variance satisfied when: \(\dot{\phi}(\xi) \leq 0, \forall \xi \in
\{\xi:\phi(\xi)=0\}\)
-
Finite time convergence satisfied when: \(\dot{\phi}(\xi) \leq - \eta, \forall \xi \in
\{\xi:\phi(\xi) > 0\}\), the robot will back into the safe set
(\(\phi(\xi) < 0\)) within finite
steps. E.g.: \[If:
\left\{
\begin{array}{l}
\phi(\xi) = a > 0 \\
\dot{\phi}(\xi) = - \eta
\end{array}
\right.
, then - \eta \cdot N + a < 0\] where N is the number
of steps.
Safe Control
This is to convert the rate of change of the safety index \(\dot{\phi}(\xi)\) to control signal \(u\).
Safe Control Signal
For the affine system, the \(u\) is
linear to \(\dot{\xi}\). We define:
\[\dot{\xi} = f(\xi)+g(\xi) \cdot u\]
where:
-
\(\xi\) is the robot state, with
definition: \[\xi =
\begin{bmatrix}
P_x\\
P_y\\
V_x\\
V_y
\end{bmatrix}\] where \(P\) is the position, \(V\) is the velocity.
-
\(\dot{\xi}\) is the rate of
change of the robot state, with definition: \[\dot{\xi} =
\begin{bmatrix}
V_x\\
V_y\\
a_x\\
a_y
\end{bmatrix}\] where \(a\) is the acceleration.
-
\(u\) is the control
signal.
Hence, we can derive the expression of the control signal: \[\dot{\xi} =
\begin{bmatrix}
V_x\\
V_y\\
a_x\\
a_y
\end{bmatrix}
=
\underbrace{
\begin{bmatrix}
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
P_x\\
P_y\\
V_x\\
V_y
\end{bmatrix}
}_{f(\xi)}
+
\underbrace{
\begin{bmatrix}
1 & 0\\
0 & 1\\
1 & 0\\
0 & 1
\end{bmatrix}
}_{g(\xi)}
\cdot u\] Therefore, the u is \([a_x \quad a_y]^T\).
Safe Control Function
According to the definition of the safety index from the previous
section: \(\phi(\xi) = d^2_{min}-d^2+k \cdot
\dot{d}\) Then, the rate of change of the safety index can be
expressed: \[\begin{aligned}
\dot{\phi}(\xi) &= \frac{\partial \phi}{\partial \xi} \cdot \dot{x}
\\
&= \frac{\partial \phi}{\partial \xi} \cdot [f(\xi)+g(\xi) \cdot
u] \\
&= \frac{\partial \phi}{\partial \xi} \cdot f(\xi) +
\frac{\partial \phi}{\partial \xi} \cdot g(\xi) \cdot u \\
&= L_f \phi + L_g \phi \cdot u
\end{aligned}\] We successfully obtained a Lie Group Derivation.
According to the constraint: \(\dot{\phi}(\xi)\leq -\eta\), then: \(\dot{\phi}(\xi)\leq -\eta \Leftrightarrow L_f
\phi + L_g \phi \cdot u \leq -\eta\) Hence, we obtain: \[u \leq \frac{-\eta-L_f \phi}{L_g \phi}\]
Now, the constraints on the safety index can be transformed into
constraints on the control signal.
Optimization of Safe
Control Function
Because the \(f(\xi)\) is
independent of the control signal, to ensure the satisfaction of the
constraint: \(L_f \phi + L_g \phi \cdot u \leq
-\eta\), we need to minimize the value of \(L_g \phi \cdot
u\). The theoretical
minimized value for \(L_g \phi \cdot
u\) occurs when the direction of two vectors \(L_g \phi\) and
\(u\) is the same, thus: \(L_g \phi \cdot
u = -\parallel L_g \phi
\parallel\) In this case, the \(L_g
\phi\) becomes the steepest descent (most safe direction). I
drawed a graph to illustrate this idea:
However, the APF method could also derive the safest direction by
finding the smallest potential direction. Also, according to the
constraint of maneuverability of the robot (like the sliding constraint
and rolling constraint), the robot’s locomotion cannot turn in the
safest direction directly. Hence, we need to apply this method to a
closed-loop control environment and optimize it.
Guoyi is still revising the ME3243 courses, which he enrolled in 1.5
years ago. Plan to finish the next section by week 6.
Weekly Report 2
From: Chen Guoyi
Sent: Thursday, February 8, 2024 at 12:17
To: Prahlad Vadakkepat; Liang Yuanchang
Cc: Chen Guoyi
Subject: [UROP] Weekly Report 2- EAPF Replication
|
Dear Professor Vadakkepat,
I hope this email finds you well.
I am writing to summarize my work from the past week and outline my plans for the upcoming weeks. Following the guidelines in Weekly Report 1, I have been progressing as scheduled. I presented last week's work to Mr. Liang during our routine weekly group meeting yesterday, where I received valuable feedback and support.
Last week, I replicated the methodology from your paper on Evolutionary Artificial Potential Fields and Their Application in Real-Time Robot Path Planning using MATLAB. Despite the two decades since its publication, the concept of artificial potential fields remains a cornerstone in solving path-planning issues. In line with the overarching project timeline, I intend to refine the artificial potential fields over the coming weeks and ultimately implement a 2D model in ROS for complex interactive environment simulation.
For record-keeping and future reference, I have attached the initial draft of my paper (0207-1230.pdf). This draft will serve as a checkpoint for content and logical flow improvements at the end of major sections.
I have uploaded the MATLAB source code, execution results, and visual outcomes to my NUS School of Computing repository. The visualization follows the same logic as presented in your EAPF paper. You may access from:
Source code: https://www.comp.nus.edu.sg/~guoyi/project/urop/code/
Simulation Demonstration (Visualized result): https://www.comp.nus.edu.sg/~guoyi/project/urop/demo/
Original dataset: https://www.comp.nus.edu.sg/~guoyi/project/urop/dataset/
Your and Mr. Liang's guidance and support have been immensely helpful. Thank you for your continued encouragement.
Wishing you and your family a joyful and prosperous Chinese New Year!
Best regards,
Guoyi
Weekly Report 1
From: Chen Guoyi
Sent: Monday, January 29, 2024 1:42 PM
To: Prahlad Vadakkepat; Liang Yuanchang
Cc: Chen Guoyi
Subject: [UROP] Weekly Report 1 – Holistic Plan
|
Dear Professor Vadakkepat,
Greetings from Guoyi. I hope this email finds you well.
This is my first weekly report, aiming to summarize my research progress from January 19 to January 28, 2024, and to outline a holistic plan for the entire project. These plans are based on my background knowledge, the assistance offered by Mr. Liang, and the literature I collected last week, ensuring a high feasibility. I look forward to receiving your approval and suggestions.
According to the proposal, our task is to enhance the feasibility of robots replacing human labor in construction industry environments and to evaluate and optimize our solutions using simulation methods. In this context, our robots need to collaborate safely with other robots or human workers. Based on my and Mr. Liang's knowledge framework and research direction, we identified the problem by researching safety control strategies for robots in complex interactive environments. The preliminary title of our paper is: "Safety Control Strategies for Autonomous Robots in Complex Interactive Environments Based on Reinforcement Learning."
The keywords covered in this paper title represent our macro research topics: safety strategies, control strategies, and reinforcement learning. Our initial focus will be on the robot's safety strategies, combining naive safety strategies with convex optimization and quadratic programming methods to make it suitable for complex interactions in a 2D plane. This safety strategy is a control function, taking SLAM environment data with multiple moving objects as input and producing a control signal as output. In response to this signal, we will model and simulate the robot, combining the kinematic equations derived from control strategies, and enhance the robot's mobility using fuzzy PID methods. In reinforcement learning, we will integrate safety and control strategies, enabling the robot to plan a safe path through the collected SLAM maps, thereby achieving safe robot control in complex environments.
The above outlines the overall research approach. I plan to maximize research efficiency by utilizing both class and extracurricular time. I will learn from meetings with you and Mr. Liang, NUS courses, external courses, and academic literature to acquire the necessary knowledge for this research. The details of the research and learning process schedule:
I have received approval from Dr. Liu Changliu, a lecturer at CMU (cliu6@andrew.cmu.edu), to use code from the CMU course "16-883 Provably Safe Robotics" for more in-depth research (licensed under GPL 2.0). I have verified this code's feasibility and portability and built a primary functional platform based on the CS3244 environment. This platform will facilitate future simulations of complex environments. You can view a video to understand the current state of the code (the safety strategy has not yet been loaded; the results are currently purely from reinforcement learning).
I will arrange my study and research tasks according to the timeline set out in the research and learning process schedule, and I am eager for your advice and assistance. I will continuously update my progress in my UROP log file. Every Wednesday, in my meetings with Mr. Liang, I will summarize the previous week's progress and confirm the research tasks for the following week. I will submit a weekly report to you every Monday for your review. This is the first report, which includes the overall timeline and research framework. I seek your permission and suggestions. If possible, please respond to this weekly report at your earliest convenience so I can continue my work upon receiving your approval.
I hope you have a lovely week ahead!
Best regards,
Chen Guoyi

